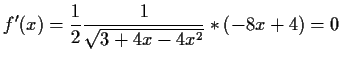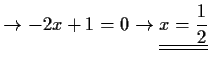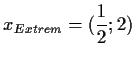- a)
-
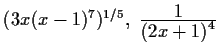 ,
, - b)
-
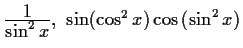 .
.
Lösung:
- a)
- (i)
-
![$\displaystyle \left[(3x(x-1)^7)^{\frac{1}{5}}\right]'$](img3.gif)
![$\displaystyle =\frac{1}{5}[3x(x-1)^7]^{-\frac{4}{5}}*[3*(x-1)^7+3x*7(x-1)^6*1]$](img4.gif)
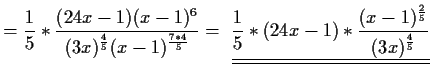
- (ii)
-
![$\displaystyle \left[(2x+1)^{-4}\right]'
=-4*(2x+1)^{-5}*2=\underline{\underline{-8(2x+1)^{-5}}}$](img6.gif)
- b)
- (i)
-
![$\displaystyle [(\sin{x})^{-2}]'=\underline{\underline{-2\frac{1}{\sin{^3x}}*\cos{x}}}$](img7.gif)
- (ii)
-
![$\displaystyle [\sin{\cos{^2x}}*\cos{\sin{^2x}}]'=u'v*uv'$](img8.gif)
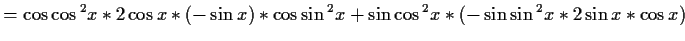
![$\displaystyle = -2\sin{x}\cos{x} [\cos{\cos{^2x}}*\cos{\sin{^2x}}+
\sin{\cos{^2x}}*\sin{\sin{^2x}}]
$](img10.gif)
![$\displaystyle = \ \underline{\underline{
-2\sin{x}\cos{x}[\cos( \cos{^2x} - \sin{^2x})]}}
$](img11.gif)
- a)
-
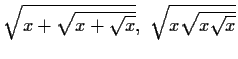
- b)
-
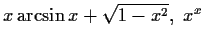
- a)
- (i)
-
![$ \left[\sqrt{x+\sqrt{x+{sqrt{x}}}}\right]'
= \frac{1}{2}*\frac{1}{\sqrt{x+\sqrt...
...}*
\left(1+\frac{1}{\sqrt{x+\sqrt{x}}}
\left(1+\frac{1}{\sqrt{x}}\right)\right)$](img14.gif)
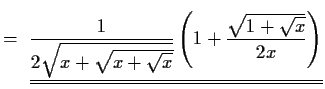
- (ii)
-
![$\displaystyle \left[\sqrt{x\sqrt{x\sqrt{x}}}\right]'=\left[\sqrt{x\sqrt{x^{\fra...
...}}}}\right]'=\left[\sqrt{x^{\frac{7}{4}}}\right]'=\left[x^{\frac{7}{8}}\right]'$](img16.gif)
![$\displaystyle =\frac{7}{8}x^{-\frac{1}{8}}
=\underline{\underline{\frac{7}{8}*\frac{1}{\sqrt[\displaystyle 8]{\displaystyle x}}}}$](img17.gif)
- b)
- (i)
-
![$\displaystyle \left[x\arcsin x + \sqrt{1-x^2}\right]'=1* \arcsin x + x*
\frac{1}{\sqrt{1-x^2}}+\frac{1}{2}*\frac{1}{\sqrt{1-x^2}}*(-2x)$](img18.gif)
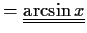
- (ii)
-
![$\displaystyle y=x^x,\quad betrachte\quad \left[\ln y =x*\ln x \right]$](img20.gif)
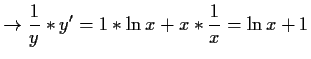
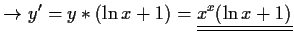
- a)
- Berechnen Sie die Ableitung von
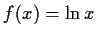 mittels des Satzes
über die Ableitung der Umkehrfunktion.
mittels des Satzes
über die Ableitung der Umkehrfunktion. - b)
- Berechnen Sie die Ableitung der
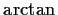 -Funktion mittels der
Ableitung der Umkehrfunktion.
-Funktion mittels der
Ableitung der Umkehrfunktion.
- a)
-
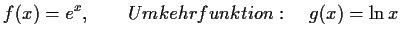
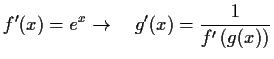
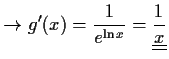
- b)
-
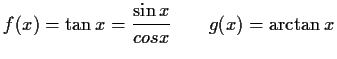

Lösung: Definitionsbereich:
Parabel nach unten offen: