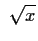Mathematik I für Chemiker
8. Serie vom 29.11.01
- 29.
- Berechnen Sie die folgenden Grenzwerte:
- a)
-
- b)
- Existiert
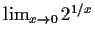 ? Begründen Sie!
? Begründen Sie!
- c)
- Existiert
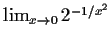 ? Begründen Sie!
? Begründen Sie!
Lösung:
- a)
-
also bei
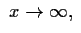
Asymptode
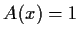
- b)
-
rechts
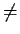
links
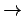
kein Grenzwert
- c)
-
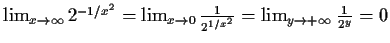
es existiert Grenzwert.
- 30.
- Ist die folgende Funktion
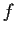 an der Stelle
an der Stelle 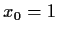 stetig oder
unstetig? Falls
stetig oder
unstetig? Falls 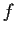 dort nicht stetig ist, wie müßte man
dort nicht stetig ist, wie müßte man 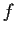 abändern, um eine stetige Funktion zu erhalten?
abändern, um eine stetige Funktion zu erhalten?
Lösung:
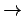
unstetig an 1
Abänderung:
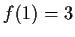
- 31.
- Bestimmen Sie wenn möglich eine Konstante
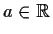 ,
so daß die Funktion
für alle
,
so daß die Funktion
für alle
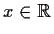 stetig wird.
stetig wird.
Lösung:
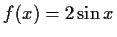 für
für
 , an Grenze also
, an Grenze also
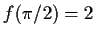
folglich muß für Stetigkeit
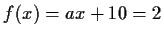 sein (bei
sein (bei 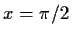 )
)
- 32.
- Berechnen Sie die folgenden Grenzwerte, sofern sie existieren:
- a)
-
- b)
-
für
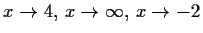 .
.
Lösung:
- a)
-
- b)
-
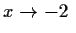
kein Grenzwert, wegen
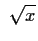
Diese Lösungsblatt wurde von Martin Zschache erstellt.
Dr.Wolfgang Quapp
2002-03-26
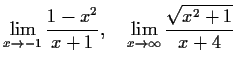
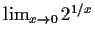 ? Begründen Sie!
? Begründen Sie!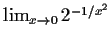 ? Begründen Sie!
? Begründen Sie!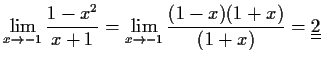
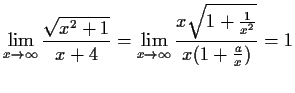 also bei
also bei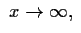 Asymptode
Asymptode 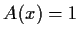
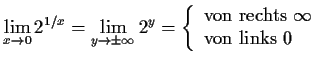 rechts
rechts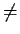 links
links 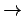 kein Grenzwert
kein Grenzwert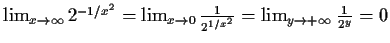
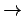 es existiert Grenzwert.
es existiert Grenzwert.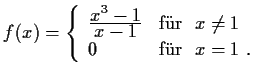
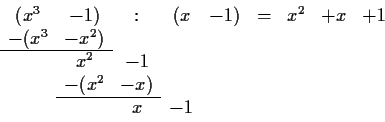
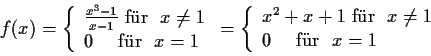
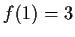
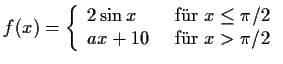
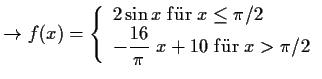
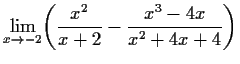
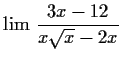
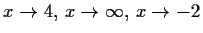 .
.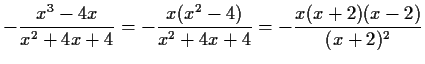
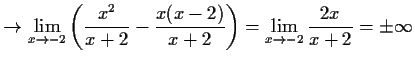
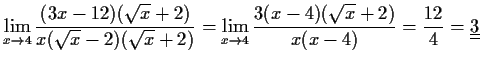
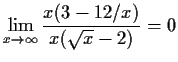
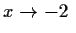 kein Grenzwert, wegen
kein Grenzwert, wegen