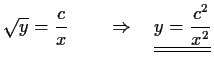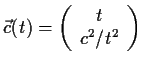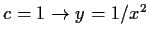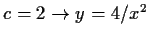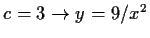Mathematik I für Chemiker
7. Serie vom 22.11.01
- 25.
- Schreiben Sie die folgenden Funktionen
 die gegeben sind durch
die gegeben sind durch
- a)
-
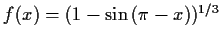 ,
,
- b)
-
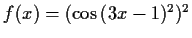 ,
,
- c)
-

als zusammengesetzte Funktionen in der Gestalt
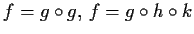 usw.
usw.
Lösung:
- a)
-
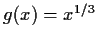 ,
, 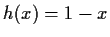 ,
,
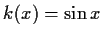 ,
,
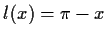
- b)
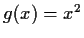 ,
,
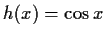 ,
, 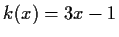
- c)
-
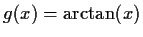 ,
,
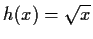 ,
,
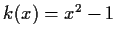
- 26.
- Bestimmen Sie die Umkehrfunktionen von
- a)
-
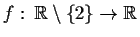 mit
mit
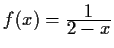 ,
,
- b)
-
 mit
mit

Lösung:
- a)
-
- b)
-
- 27.
- Bestimmen Sie eine Parameterdarstellung
a) des Graphen von
![$ f:\, [-2,2] \to \mathbb {R},\ f(x) = x^2$](img29.gif) ,
,
b) des Streckenzuges von 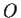 über
über
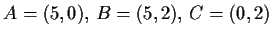 nach
nach 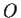 .
.
Lösung:
a)
b)
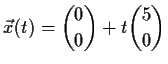 für
für 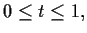
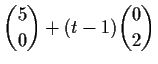 für
für 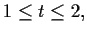
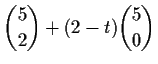 für
für 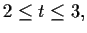
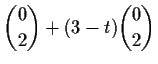 für
für 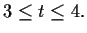
- 28.
- Die Funktion
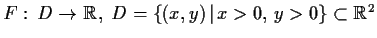 mit
mit
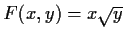 sei gegeben. Die
Niveaumenge
sei gegeben. Die
Niveaumenge
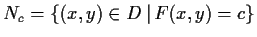 ist Graph einer
Funktion
ist Graph einer
Funktion
 . Wie lautet diese Funktion?
Skizzieren Sie zu den Werten
. Wie lautet diese Funktion?
Skizzieren Sie zu den Werten
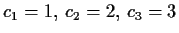 die
zugehörigen Kurven. Wie lautet eine Parameterdarstellung von
die
zugehörigen Kurven. Wie lautet eine Parameterdarstellung von
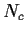 ?
?
Lösung:
Sei
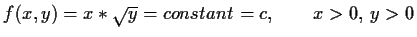 also
also
Parameterdarstellung:
Diese Lösungsblatt wurde von Martin Zschache erstellt.
Dr.Wolfgang Quapp
2002-03-26
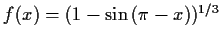 ,
,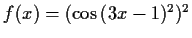 ,
,
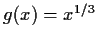 ,
, 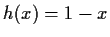 ,
,
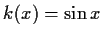 ,
,
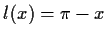
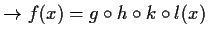
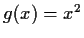 ,
,
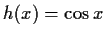 ,
, 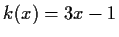
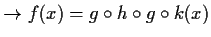
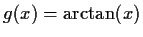 ,
,
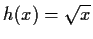 ,
,
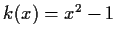
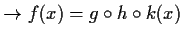
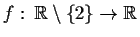 mit
mit
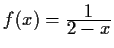 ,
, mit
mit


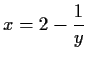
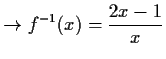
![$\displaystyle \tan{y}=\sqrt[\displaystyle 3]{\frac{1+x}{1-x}},\quad\tan{^3y}
=\frac{1+x}{1-x}$](img26.gif)
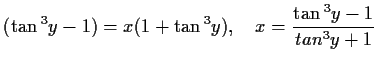
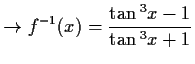
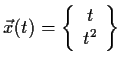
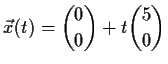 für
für 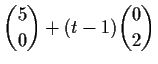 für
für 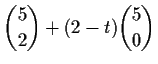 für
für 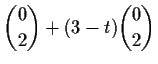 für
für ![]() also
also