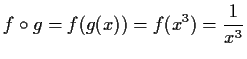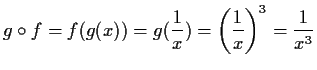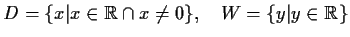Lösung: Nullpunkt:
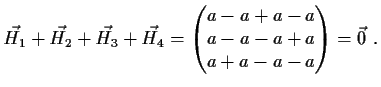
- a)
- Welchen Winkel bilden die folgenden Vektoren des
 miteinander? Wie groß ist der Flächeninhalt des von ihnen aufgespannten
Parallelogramms?
Lösung:
miteinander? Wie groß ist der Flächeninhalt des von ihnen aufgespannten
Parallelogramms?
Lösung: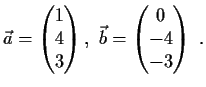
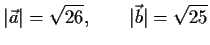
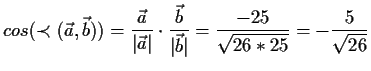 Der Komplementwinkel ist dann 11,31
Der Komplementwinkel ist dann 11,31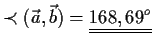
 .
.
- b)
- Für welches
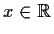 sind die Vektoren
orthogonal?
sind die Vektoren
orthogonal?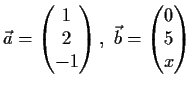
Lösung: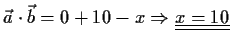
- a)
-
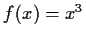 ,
, - b)
-
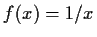 ,
, - c)
-
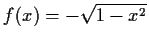 ,
, - d)
-
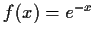 ,
, - e)
-
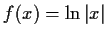 ,
, - f)
-
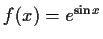 ,
, - g)
-
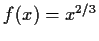 ,
, - h)
-

- a)
-
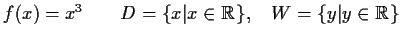
- b)
-
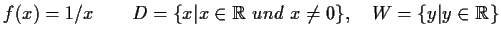
- c)
-
![$ f(x) = -\sqrt{1-x^2} \qquad D=\{x\vert x\in[-1;1]\},\quad
W=\{y\vert y\in[-1;0]\}$](img23.gif)
- d)
-
![$ f(x) = e^{-x} \qquad D=\{x\vert x\in\mathbb {R}\},\quad
W=\{y\vert y\in[0;\infty]\} $](img24.gif)
- e)
-
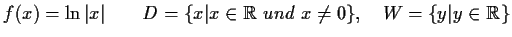
- f)
-
![$ f(x) = e^{\sin x} \qquad D=\{x\vert x\in\mathbb {R}\},\quad
W=\{y\vert y\in[\frac{1}{e};e]\} $](img26.gif)
- g)
-
![$ f(x) = x^{2/3} \qquad D=\{x\vert x\in\mathbb {R}\},\quad
W=\{y\vert y\in[0;\infty]\} $](img27.gif)
- h)
-
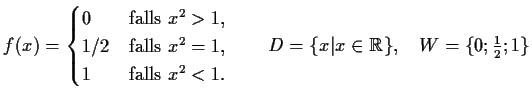
- a)
- Bestimmen Sie die inverse Funktionen zu
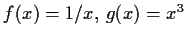 und deren Definitions- und Wertebereich.
und deren Definitions- und Wertebereich.
Lösung:
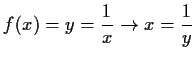 Vertauschen der Variablen
Vertauschen der Variablen
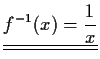
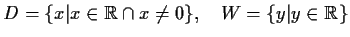
![$\displaystyle g(x)=y=x^3 \to \sqrt[\displaystyle 3]{y}=x$](img33.gif) Vertauschen der Variablen
Vertauschen der Variablen
![$\displaystyle \underline{\underline{g^{-1}(x)=\sqrt[\displaystyle 3]{x}}}$](img34.gif)
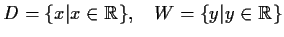
- b)
- Berechnen Sie
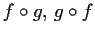 mit Definitions- und
Wertebereich.
mit Definitions- und
Wertebereich.
Lösung: