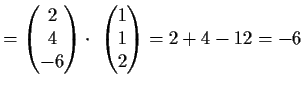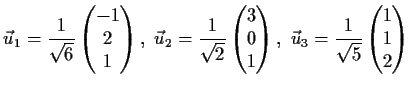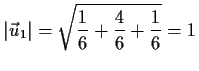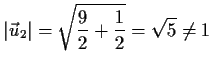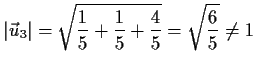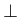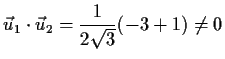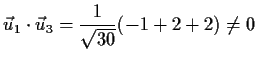Mathematik I für Chemiker
5. Serie vom 08.11.01
- 17.
- a)
- Begründen Sie, warum die Vektoren
keine Basis des
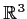 bilden können.
bilden können.
Lösung:
Die 4 Vektoren des
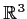 sind linear abhängig:
wird erfüllt durch
sind linear abhängig:
wird erfüllt durch
Dabei ist
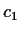
beliebig, und
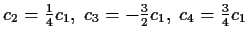
.
- b)
- Wählen Sie aus den Vektoren in Teil a) eine Basis des
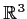 aus.
aus.
Lösung:
Gleichungen:
- 1
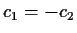
- 2
-
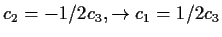
- 3
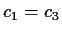
- 18.
- Berechnen Sie
 für die Vektoren
für die Vektoren
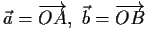 , wobei die Punkte
, wobei die Punkte 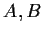 bezüglich eines rechtwinkligen kartesischen Koordinatensystems gegeben sind
durch
bezüglich eines rechtwinkligen kartesischen Koordinatensystems gegeben sind
durch
 . Stellen Sie die drei Vektoren auch
graphisch dar.
. Stellen Sie die drei Vektoren auch
graphisch dar.
Lösung:
- 19.
- Bestimmen Sie das Volumen des von den drei Vektoren
aufgespannten Spats.
Lösung:
- 20.
- Prüfen Sie, ob die drei Vektoren
eine Orthonormalbasis des
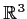 bilden.
bilden.
Lösung: nein, weil
- a)
- Betrag nicht immer 1
- b)
- nicht
Diese Lösungsblatt wurde von Martin Zschache erstellt.
Dr.Wolfgang Quapp
2002-03-26
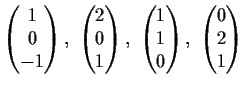
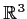 bilden können.
bilden können.
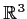 sind linear abhängig:
wird erfüllt durch
sind linear abhängig:
wird erfüllt durch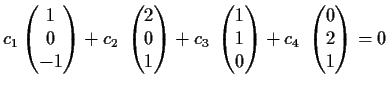
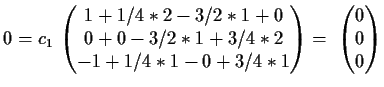 Dabei ist
Dabei ist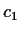 beliebig, und
beliebig, und
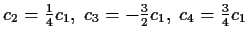 .
.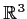 aus.
aus.
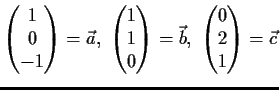 Gleichungen:
Gleichungen: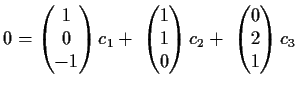
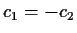
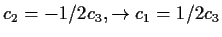
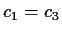
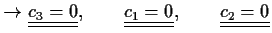
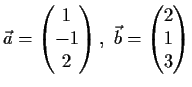
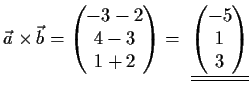
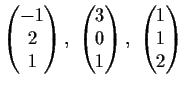
![$\displaystyle V=\left[
\begin{pmatrix}
-1 \\
2 \\
1 \end{pmatrix}\times\
\be...
...\\
1 \end{pmatrix}\right] \cdot \
\begin{pmatrix}
1 \\
1 \\
2 \end{pmatrix}$](img20.gif)