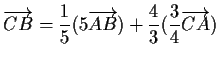- a)
- Man drücke
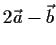 als Linearkombination von
als Linearkombination von
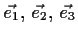 aus.
aus.
Lösung:
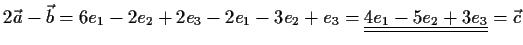
- b)
- Man bestimme den Einheitsvektor in Richtung von
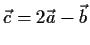 .
.
Lösung:
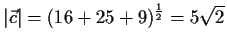
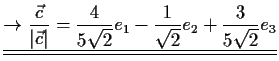
- a)
- wie weit, und
- b)
- in welcher Richtung
Lösung:
- 1
-
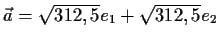
- 2
-
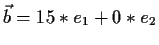
- 3
-

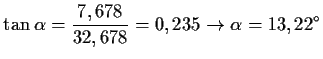
Lösung:
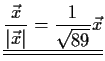
Lösung:
Wenn A,B,C kollinear sind, so sind je 2 Vektoren linear abhängig.
Annahme: Seien A,B,C nicht kollinear, dann ist