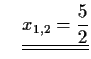- a)
- Schreiben Sie diese Zahlen in der Gestalt
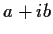 ,
, - b)
- Stellen Sie diese Zahlen in der Gaußschen Zahlenebene dar,
- c)
- Stellen Sie diese Zahlen in der Exponentialdarstellung dar,
- d)
- Berechnen Sie
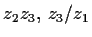 .
.
Lösung:
- a)
-
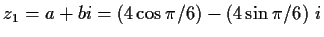
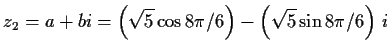
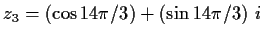
- c)
-
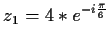
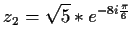
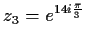
- d)
-
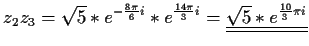
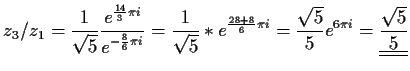
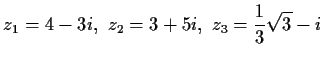
- a)
- Schreiben Sie diese Zahlen in ihrer trigonometrischen Form,
- b)
- Stellen Sie diese Zahlen in der Gaußschen Zahlenebene dar,
- c)
- Stellen Sie diese Zahlen in der Exponentialdarstellung dar,
- d)
- Berechnen Sie
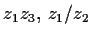 .
.
Lösung:
- d)
-
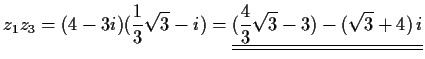

- a)
- Schreiben Sie diese Zahlen in der Gestalt
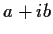 ,
, - b)
- Stellen Sie diese Zahlen in der Gaußschen Zahlenebene dar,
- c)
- Stellen Sie diese Zahlen in ihrer trigonometrischen Gestalt dar,
- d)
- Berechnen Sie
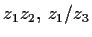 .
.
Lösung:
- d)
-
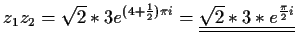
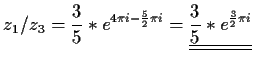
- a)
- Berechen Sie die Nullstellen des Polynoms
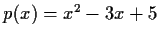 ,
geben Sie ihre Vielfachheiten an und stellen Sie das Polynom als Produkt von
Linearfaktoren dar.
,
geben Sie ihre Vielfachheiten an und stellen Sie das Polynom als Produkt von
Linearfaktoren dar. - b)
- Berechen Sie die Nullstellen des Polynoms
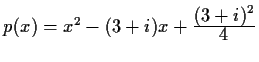 , geben Sie ihre Vielfachheiten an und stellen Sie das
Polynom als Produkt von zwei Linearfaktoren dar.
, geben Sie ihre Vielfachheiten an und stellen Sie das
Polynom als Produkt von zwei Linearfaktoren dar. - c)
- Berechen Sie die Nullstellen des Polynoms
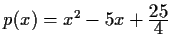 , geben Sie ihre Vielfachheiten an und stellen Sie das
Polynom als Produkt von Linearfaktoren dar..
, geben Sie ihre Vielfachheiten an und stellen Sie das
Polynom als Produkt von Linearfaktoren dar..
Lösung:
- a)
-
0 
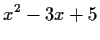
(1) 
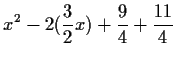
(2) 
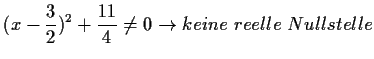
(3) 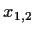

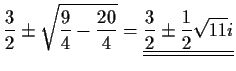
(4) 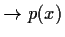

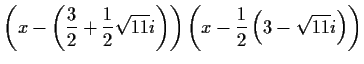
(5) - b)
-

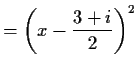

- c)
-
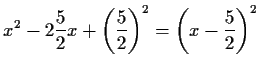
 Doppelnullstelle
Doppelnullstelle