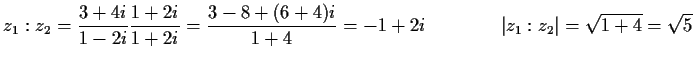Hinweis: Stellen Sie die Wahrheitstabelle auf für
![]() .
.
Lösung:
Wir haben die Wahrheitstabelle:
| - | - | a | - | - | b |
| p | q |
|
r | s |
|
| w | w | w | w | w | w |
| w | f | f | w | f | w |
| f | f | f | f | w | w |
| f | w | f | f | f | f |
Ist in der Implikation
- a)
- Geben Sie die folgenden Funktionen an:
- (i)
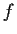 ordnet jeder reellen Zahl ihre dritte Potenz zu,
ordnet jeder reellen Zahl ihre dritte Potenz zu,- (ii)
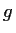 ordnet jeder reellen Zahl die Zahl
ordnet jeder reellen Zahl die Zahl 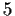 zu,
zu,- (iii)
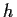 ordnet jeder nicht positiven reellen Zahl die Zahl
ordnet jeder nicht positiven reellen Zahl die Zahl 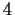 zu und
jeder positiven reellen Zahl ihr Quadrat.
zu und
jeder positiven reellen Zahl ihr Quadrat.- (iv)
- Bestimme
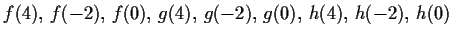
- b)
- Welche der Funktionen aus a) ist (sind) injektiv?
- c)
- Geben Sie die Definitions- und Wertebereiche an.
Lösung:
- (i)
-
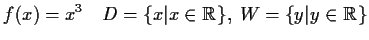
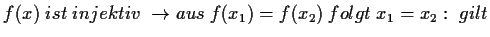
- (ii)
-
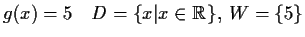 nicht injektiv
nicht injektiv - (iii)
-
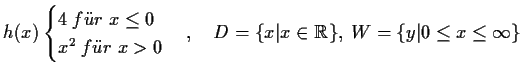 nicht injektiv
nicht injektiv - (iv)
-
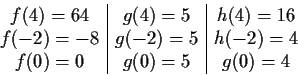
Lösung: