Lösung:
![]() D ist die Dissoziationsenergie,
D ist die Dissoziationsenergie, ![]() der Kernabstand mit der geringsten
potentiellen Energie
der Kernabstand mit der geringsten
potentiellen Energie
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Nullstellen ![]()
![]()
![]()
![]()
![]()
![]()
![]() Die Funktion hat eine Nullstelle bei
Die Funktion hat eine Nullstelle bei ![]()
Extremwerte
Notwendige Bedingung ![]()
![]()
![]()
![]()
![]()
![]() (mögliche Extremstelle)
(mögliche Extremstelle)
Hinreichende Bedingung
![]()
![]()
![]()
![]()
![]() Minimum
Minimum
Die Funktion hat an der Stelle ![]() ein lokales Minimum
ein lokales Minimum
![]()
Wendepunkte
Notwendige Bedingung ![]()
![]()
![]()
![]()
![]()
![]()
![]() (mögliche Wendestelle)
(mögliche Wendestelle)
Hinreichende Bedingung
![]()
![]()
![]()
![]()
![]()
![]()
Die Funktion V hat an der Stelle
![]() eine Wendestelle
eine Wendestelle
![]()
Grenzwerte
![]()
Konvexität
(nach oben) Konkav: ![]()
![]()
![]()
![]()
![]()
![]()
(nach oben) Konvex: ![]()
![]()
![]()
![]()
![]()
![]()
Für
![]() ist der Graph der Funktion nach oben konkav
bzw. nach unten konvex,
ist der Graph der Funktion nach oben konkav
bzw. nach unten konvex,
für
![]() ist der Graph der Funktion nach unten konkav
bzw. nach oben konvex.
ist der Graph der Funktion nach unten konkav
bzw. nach oben konvex.
Monotonie
streng monoton steigend: ![]()
![]()
![]()
![]()
![]()
![]()
streng monoton fallend: ![]()
![]()
![]()
![]()
![]()
![]()
Die Funktion V ist für ![]() streng monoton fallend und für
streng monoton fallend und für ![]() streng monoton steigend. An der Stelle
streng monoton steigend. An der Stelle ![]() hat sie ein absolutes
Minimum.
hat sie ein absolutes
Minimum.
Lösung:
![]()
![]()
![]()
![]()
Schnittpunkt:
![]()
![]()
![]()
![]()
Steigung der Tangenten:
![]()
![]()
Spitzer Winkel zwischen den beiden Funktionen

![]()
- a)
-
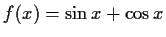 ,
, - b)
-
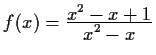
Lösung:
- a)
-
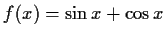 Periode:
Periode: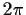
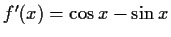
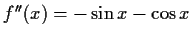
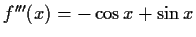
![$ W=[-\sqrt{2};\sqrt{2}]$](img98.gif)
Nullstellen
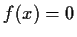
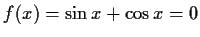
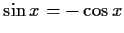
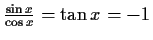
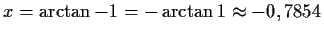
Tangensfunktionen haben die Periode , daher gibt es Nullstellen
bei
, daher gibt es Nullstellen
bei
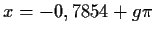 .
.
Die Funktion f hat periodisch Nullstellen: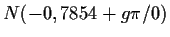 .
.
Extremwerte
Notwendige Bedingung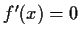
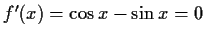
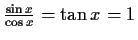
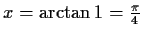
mögliche Extremstellen bei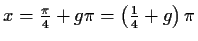
Hinreichende Bedingung
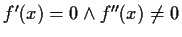
Da die Funktion f die Periode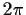 hat, müssen zwei Möglichkeiten
unterschieden werden:
hat, müssen zwei Möglichkeiten
unterschieden werden:
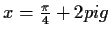 und
und
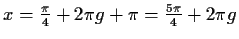
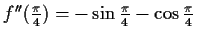
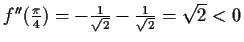 (Maximum)
(Maximum)
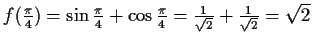
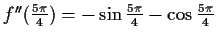
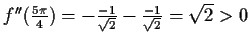 (Minimum)
(Minimum)
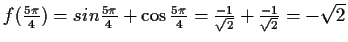
Die Funktion f hat periodisch an den Stellen
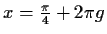 lokale
Maxima
lokale
Maxima
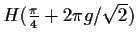
und an den Stellen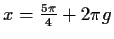 lokale Minima
lokale Minima
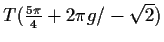
Wendepunkte
Notwendige Bedingung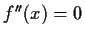
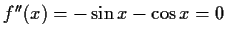
 Periode
Periode
Hinreichende Bedingung
Es muss zwischen zwei Möglichkeiten unterschieden werden:
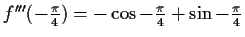
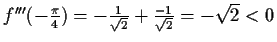
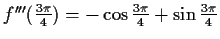
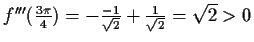
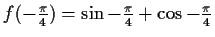
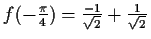
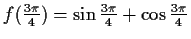
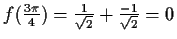
Die Funktion hat periodisch Wendestellen
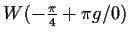
Grenzwerte
![$ \lim_{x\to\pm\infty}f(x)=\lim_{x\to\pm\infty}[\sin{x}+\cos{x}] \to$](img138.gif) unbestimmbar, es existiert kein Grenzwert.
unbestimmbar, es existiert kein Grenzwert.
Konvexität
Konkave Seite nach oben bzw. konvexe nach unten: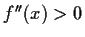
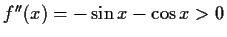
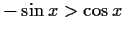
![$ [-\frac{\sin{x}}{\cos{x}}>1\wedge \cos{x}>0]\vee
[-\frac{\sin{x}}{\cos{x}}=\ta...
...-1\wedge \cos{x}<0]\vee[\sin{x}<0 \wedge
(x=\frac{\pi}{2}\vee x=\frac{3\pi}{2}]$](img142.gif)
Da die Funktion f die Periode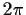 hat, braucht man nur ein Intervall der
Größe
hat, braucht man nur ein Intervall der
Größe 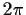 betrachten: z.B.:
betrachten: z.B.:
![$ x\in[-\frac{\pi}{4};\frac{7\pi}{4}]$](img143.gif)
![$ [(\frac{\pi}{2}<x<\frac{3\pi}{4} \vee \frac{3\pi}{2}<x<\frac{7\pi}{4})
\wedge ...
...frac{3\pi}{2}) \wedge (\frac{\pi}{2}<x<\frac{3\pi}{2})]
\vee [x=\frac{3\pi}{2}]$](img144.gif)
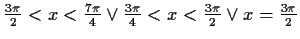
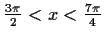
Konkave Seite nach unten bzw. konvexe nach oben:
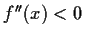
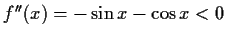
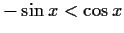
![$ [-\frac{\sin{x}}{\cos{x}}>1 \wedge \cos{x}<0] \vee
[-\frac{\sin{x}}{\cos{x}}<1 \wedge \cos{x}>0] \vee
[\sin{x}>0\wedge \cos{x}=0]$](img150.gif)
![$ [\frac{\sin{x}}{\cos{x}}=\tan{x}<1 \wedge \cos{x}<0]\vee
[\frac{\sin{x}}{\cos{...
...\wedge \cos{x}>0] \vee [\sin{x}>0 \wedge
(x=\frac{\pi}{2}\vee x=\frac{3\pi}{2})$](img151.gif)
Da die Funktion f die Periode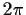 hat, braucht man nur ein Intervall der
Größe
hat, braucht man nur ein Intervall der
Größe 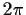 betrachten: z.B.:
betrachten: z.B.:
![$ x\in[-\frac{\pi}{4};\frac{7\pi}{4}]$](img143.gif)
![$ [(\frac{\pi}{2}<x<\frac{3\pi}{4} \vee \frac{3\pi}{2}<x<\frac{7\pi}{4})
\wedge ...
...<\frac{\pi}{2} \vee \frac{3\pi}{2}<x\le
\frac{7\pi}{4})] \vee [x=\frac{\pi}{2}]$](img152.gif)
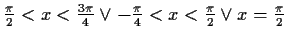
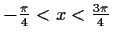
Für
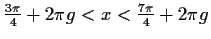 ist der Graph nach oben
konkav,
ist der Graph nach oben
konkav,
für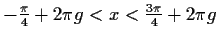 ist der Graph nach
unten konkav bzw. nach oben konvex, an den Stellen
ist der Graph nach
unten konkav bzw. nach oben konvex, an den Stellen
 hat die Funktion Wendestellen.
hat die Funktion Wendestellen.
Monotonie
Streng monoton wachsend: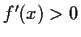
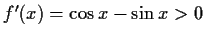
![$ [\frac{\sin{x}}{\cos{x}}=\tan{x}<1 \wedge \cos{x}>0] \vee
[\frac{\sin{x}}{\cos{x}}=\tan{x}>1 \wedge \cos{x}<0] \vee [\sin{x}<0 \wedge
\cos{x}=0]$](img160.gif)
Da die Funktion f die Periode hat, braucht man nur ein Intervall der
Größe
hat, braucht man nur ein Intervall der
Größe 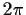 zu betrachten: z.B.:
zu betrachten: z.B.:
![$ x\in [\frac{\pi}{4};\frac{9\pi}{4}]$](img161.gif)
![$ [(\frac{\pi}{2}<x<\frac{5\pi}{4} \vee \frac{3\pi}{2}<x<\frac{9\pi}{4})
\wedge ...
...}
\vee \frac{5\pi}{4}<x<\frac{3\pi}{2})\wedge
(\frac{\pi}{2}<x<\frac{3\pi}{2})]$](img162.gif)
![$ [\frac{3\pi}{2}<x<\frac{9\pi}{4}]\vee[\frac{5\pi}{4}<x<\frac{3\pi}{2}]\vee[x=\frac{3\pi}{2}]$](img163.gif)
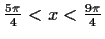
Streng monoton fallend:
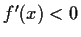
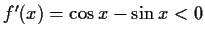
![$ [\frac{\sin{x}}{\cos{x}}=\tan{x}<1 \wedge
\cos{x}<0]\vee[\frac{\sin{x}}{\cos{x}}=\tan{x}>1\wedge\cos{x}<0]\vee[\sin{x}>0\wedge\cos{x}=0]$](img167.gif)
Da die Funktion f die Periode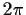 hat, braucht man nur ein Intervall der
Größe
hat, braucht man nur ein Intervall der
Größe 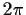 zu betrachten: z.B.;
zu betrachten: z.B.;
![$ x\in [\frac{\pi}{4};\frac{9\pi}{4}]$](img161.gif)
![$ [(\frac{\pi}{2}<x<\frac{5\pi}{4} \vee
\frac{3\pi}{2}<x<\frac{9\pi}{4})\wedge(\...
...\le
x<\frac{\pi}{2}\vee\frac{3\pi}{2}<x\le\frac{9\pi}{4}=]\vee[x=\frac{\pi}{2}]$](img168.gif)
![$ [\frac{\pi}{2}x\frac{5\pi}{4}]\vee[\frac{\pi}{4}<x<\frac{\pi}{2}]\vee[x=\frac{\pi}{2}]$](img169.gif)
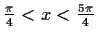
Die Funktion f ist für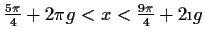 streng monoton
steigend und für
streng monoton
steigend und für
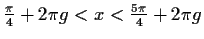 streng
monoton fallend.
streng
monoton fallend.
- b)
- a)
- Wo sind die folgenden Funktionen stetig? (Begründung!)
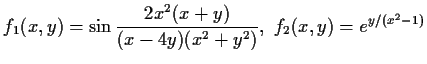
- b)
- Bestimmen Sie für die folgenden Funktionen die partiellen
Ableitungen 1. Ordnung und den Gradienten:
- i)
-
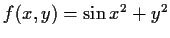 ,
, - ii)
-
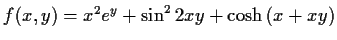
- iii)
-
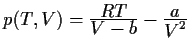 (van der
Waalsche Zustandsgleichung für Gase).
(van der
Waalsche Zustandsgleichung für Gase).
