Hinweis: Der Zerfall wird durch die Funktion
Lösung:
Es gilt
Dividiert man durch
also ist
Nach Aufgabenstellung erhält man den Ansatz
Geht man analog vor, so folgt die gesuchte Zeit (in Tagen):
Das sind 9 Stunden 55 Minuten und 59 Sekunden.
Lösung:
Nach der Binomialentwicklung ist
![]() der Koeffizient bei
der Koeffizient bei ![]() und
und
![]() der Koeffizient bei
der Koeffizient bei ![]() . Es gilt also
. Es gilt also
Außerdem hat man auf Grund der Symmetrie
Somit ist
eine Lösung, (man kann sogar leicht einsehen, daß es die einzige Lösung ist) also ist
a) Geben Sie 2 mögliche Verteilungen der Stare auf die Bäume an.
b) Bestimmen Sie die Anzahl der Verteilungen der Stare auf die Bäume.
Lösung:
a) Folgende Tabelle enthält zwei Lösungen:
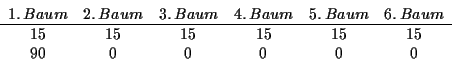
b) Die Bäume kann man als Zellen und die Stare als nichtunterscheidbere Kugeln interpretieren. So ist jede Aufteilung eine Aufteilung von
Möglichkeiten.
a) Bestimmen Sie die Reproduktionsfunktion
b) Zeichnen Sie in einem Koordinatensystem die Reproduktionsfunktion, ihre Fixpunkte und drei Werte der Folge mit Anfangswert
c) Zeigen Sie, dass
d) Zeigen Sie, dass
e) Zeigen Sie, dass die Folge
wegen c) und d) monoton fallend ist.
f) Schließen Sie aus d) und e), daß für alle Anfangswerte
g) Bestimmen Sie den Grenzwert dieser Folge und alle Anfangswerte
Lösung:
- a)
- Die Reproduktionsfunktion lautet:
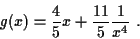
Der Fixpunkt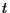 erfüllt die Gleichung
erfüllt die Gleichung
Wird von dieser Gleichung (von beiden Seiten)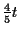 subtrahiert,
und mit
subtrahiert,
und mit 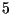 multipliziert, so ergibt sich
multipliziert, so ergibt sich
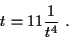
Daraus folgt
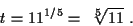
- b)
- c)
- Die Ungleichung
wird genauso behandelt wie Gleichung (1). Es ergibt sich
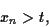
also eine wahre Aussage. Da alle Schritte umkehrbar sind folgt (2). - d)
- Man bestimmt das Minimum der Funktion
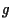 . Es gilt
. Es gilt
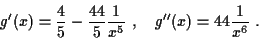
Dann verschwindet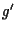 nur an der Stelle
nur an der Stelle 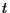 , d. h.
, d. h. 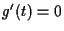 . Außerdem
gilt
. Außerdem
gilt 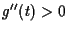 . Somit liegt in
. Somit liegt in 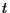 ein lokales Minimum. Wegen
ein lokales Minimum. Wegen
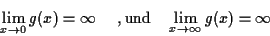
ist das Minimum sogar global. - e)
- Nach d) gilt für alle
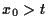 auch
auch 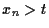 . Nun zeigt c), dass die
Folge
. Nun zeigt c), dass die
Folge
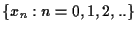 monoton fallend ist.
monoton fallend ist. - f)
- Nach d) ist zumindestens
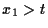 . Nach f)
ist die Folge
. Nach f)
ist die Folge
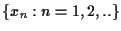 monoton fallend, und
nach d) von unten beschränkt. Also ist sie konvergent.
monoton fallend, und
nach d) von unten beschränkt. Also ist sie konvergent. - g)
- Grenzwerte und Anfangswerte
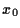 , die alle Glieder konstant lassen, sind
allgemein Fixpunkte. Also folgt
, die alle Glieder konstant lassen, sind
allgemein Fixpunkte. Also folgt
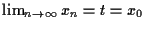
a) Entscheiden Sie mit Hilfe des Korrelationskoeffizienten, welche der Ansätze (i)
b) Bestimmen Sie mit Hilfe der Methode der kleinsten Quadrate die bessere Anpassung.
c) Zeichnen Sie die Punktwolke und die beste Anpassung in einem Koordinatensystem für einen Wert von
Lösung:
Da ![]() eine Konstante ist, ist der Korrelationskoeffizient zwischen
eine Konstante ist, ist der Korrelationskoeffizient zwischen ![]() und
und
![]() , und zwischen
, und zwischen ![]() und
und ![]() gleich, d.h.
gleich, d.h.
![]() .
Analog folgt
.
Analog folgt
![]() ,
wir können also den Fall h=0 betrachten. Dies realisiert die Transformation zu
,
wir können also den Fall h=0 betrachten. Dies realisiert die Transformation zu
![]() .
Folgende Tabelle enthält Hilfsresultate zur Berechnung der
Korrelationskoeffizienten:
.
Folgende Tabelle enthält Hilfsresultate zur Berechnung der
Korrelationskoeffizienten:
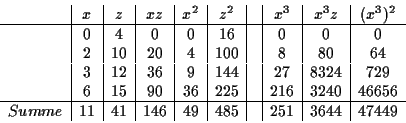
Es ergeben sich nun die Korrelationskoeffizienten aus
und
Folglich ist
und somit ist die Anpassung (i) die bessere.
b) Die beste Anpassung
folglich genügt es
Die beste Anpassung hat die Gestalt
c)
a) Bestimmen Sie folgende Charakteristiken: Modalwert, Mittelwert, empirische Varianz
b) Bestimmen Sie die Ausreißer und dann die Kenngrößen des Boxplots. Zeichnen Sie den Boxplot.
Lösung:
Zur Bestimmung von ![]() und
und
![]() dient folgende Tabelle:
dient folgende Tabelle:

Also ergeben sich mit n=40
Zur Bestimmung des Quantils der Ordnung
Die nächst größere ganze Zahl ist
b) Durch folgende Tabelle bestimmt man die Quantile:
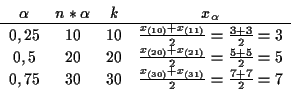
Es gilt für die Grenzen:
Somit sind die beiden Werte 18 Ausreißer. Durch folgende Tabelle bestimmt man die Quantile nach Elimination der Ausreißer mit n=38:
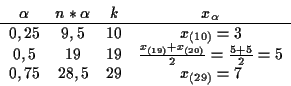
(Also ändern sich die Quantile hier nicht.)
b) Bestimmen Sie mit Hilfe des Newtonschen Verfahrens mit
c) Welche Genauigkeit hat
Lösung:
a) Die Lösung der Gleichung ![]() ist gleichwertig mit der Nullstelle
der stetigen Funktion
ist gleichwertig mit der Nullstelle
der stetigen Funktion
Es ist
b) Wegen
Es folgt somit
und
c) Zunächst wird
bestimmt. Dazu berechnet man
Im Intervall [0,5;1] ist
![\includegraphics [width=6cm,angle=270]{s.ps}](img47.gif)
![\includegraphics [width=6cm,angle=270]{s1.ps}](img85.gif)
![\includegraphics [width=6cm,angle=270]{s2.ps}](img100.gif)