Dr.Quapp: Statistik für Mathematiker mit SPSS
13. Übung - 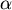 - und
- und 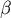 -Fehler,
KS-Test und MW-Vergleich -
-Fehler,
KS-Test und MW-Vergleich -
- 1.
- Wir stellen uns folgende Situation vor: Eine Münze sei entweder
"ehrlich", d.h.
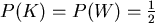 ,
oder gewichtsmäßig unsymmetrisch mit
,
oder gewichtsmäßig unsymmetrisch mit
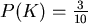 , und
, und
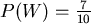 .
Durch
.
Durch  Stichproben für
Stichproben für 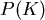 soll dies geklärt werden. Dabei
sei als kritischer Wert
soll dies geklärt werden. Dabei
sei als kritischer Wert 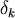 =0.4 gewählt, der Mittelwert von
=0.4 gewählt, der Mittelwert von
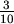 und
und  . Wie groß muß der
Stichprobenumfang
. Wie groß muß der
Stichprobenumfang  sein, um bei
sein, um bei
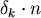 als kritische Grenze
der Stichprobe eine 95%-ige
Sicherheit
gegen den
als kritische Grenze
der Stichprobe eine 95%-ige
Sicherheit
gegen den 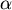 -Fehler zu haben? Ist dies wegen der Symmetrie
von
-Fehler zu haben? Ist dies wegen der Symmetrie
von 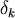 dann auch die analoge Grenze des
dann auch die analoge Grenze des 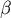 -Fehlers nach unten?
Begründen Sie die Aussage und versuchen Sie eine Lösung mit SPSS!
-Fehlers nach unten?
Begründen Sie die Aussage und versuchen Sie eine Lösung mit SPSS!
- 2.
- a) Erzeugen Sie mit Hilfe der Funktion RV.NORMAL 222 nach
N(0,1000) normalverteilte Zufallszahlen als Variable NN.
b) Zeichnen Sie mit Hilfe von STREUDIAGRAMM die empirische
Verteilungsfunktion von NN, sowie die theoretische Verteilungsfunktion von
N(0,1000), und bilden Sie die Differenz beider Funktionen.
c) Vergleichen Sie das Resultat mit dem Kolmogorov-Smirnov Test
für NN.
- 3.
- Laden Sie die Daten von Z
 : rheuma.sav. Es soll geprüft
werden, ob die Merkmale für
: rheuma.sav. Es soll geprüft
werden, ob die Merkmale für 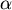 2-Globulin Lc10
2-Globulin Lc10 und Lc10
und Lc10 Mittelwertunterschiede aufweisen.
Mittelwertunterschiede aufweisen.
Anleitung: Zuerst ist zu prüfen, ob beide Merkmale normalverteilt sind
(KS-Test). Nutzen Sie dabei die Option  Fallweiser
Ausschluß.
Fallweiser
Ausschluß.
Für den Test selbst verwende man den T-Test bei gepaarten Stichproben.
Die Antwort soll zu einem Signifikanzniveau 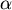 =0.05 erfolgen.
=0.05 erfolgen.
Dr.Wolfgang Quapp
2005-01-10
![]() - und
- und ![]() -Fehler,
KS-Test und MW-Vergleich -
-Fehler,
KS-Test und MW-Vergleich -