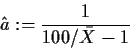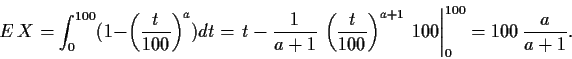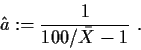Dr.Quapp: Statistik für Mathematiker mit SPSS,
HS 2001
- Freitag, 15 Uhr, Computerkabinett 4-24 HG -
Uhr, Computerkabinett 4-24 HG -
http://www.mathematik.uni-leipzig.de/MI/quapp/uebungSPSS.html
Hinweise zur 11. Übung - Stichproben u.s.w.-
1.]
Für die Gewichte von Warenpackungen wird angenommen, dass sie
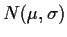 -verteilt sind mit unbekannten
-verteilt sind mit unbekannten 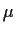 und
und 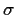 .
Es ergaben sich für eine Stichprobe vom Umfang
.
Es ergaben sich für eine Stichprobe vom Umfang 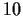 folgende Gewichte (in
kg):
folgende Gewichte (in
kg):
20,40,
20,25
20,00,
19,80,
20,05,
19,90,
20,50,
20,15,
20,20,
20,10.
Man bestimme ein Schätzintervall der Form 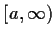 für
für 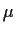 zum
Niveau
zum
Niveau 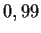 .
.
Die Teststatistik in diesem Fall ist der 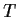 -Test
-Test
Es ist
Es ist somit das Intervall
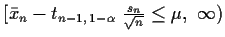 gesucht. Um das einseitige
Intervall zu berechnen, kann man den Trick anwenden, ein doppelt so
großes zweiseitiges Intervall von 2% zu betrachten, was ja 1% auf
jeder Seite bedeutet. SPSS ergibt 98% CI für den Mittelwert
(19.9434;20.3266). Eine Tabelle für die
gesucht. Um das einseitige
Intervall zu berechnen, kann man den Trick anwenden, ein doppelt so
großes zweiseitiges Intervall von 2% zu betrachten, was ja 1% auf
jeder Seite bedeutet. SPSS ergibt 98% CI für den Mittelwert
(19.9434;20.3266). Eine Tabelle für die 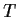 -Verteilung ergibt mit
-Verteilung ergibt mit 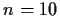 den kritischen Wert
den kritischen Wert
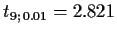 .
Der Mittelwert der Daten ist
20.135, die Standardabweichung ist 0.2148, der Standardfehler also 0.0679.
Die gesuchte linke Intervallgrenze ist also
20.135 - 2.821
.
Der Mittelwert der Daten ist
20.135, die Standardabweichung ist 0.2148, der Standardfehler also 0.0679.
Die gesuchte linke Intervallgrenze ist also
20.135 - 2.821
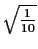 0.2148 = 19.943 .
0.2148 = 19.943 .
2.]
Geben Sie folgendes Programm in SPSS ein .
MATRIX.
COMPUTE a={2,10,3,5;1,15,2,4;3,12,5,3;2,20,4,5}.
PRINT a.
COMPUTE c={1180;1001;1507;1574}.
Print c.
COMPUTE x=INV(a)*c.
PRINT x.
compute y=a*x.
Print y .
END MATRIX.
Was bewirkt das Programm?
Kann man die Eigenwerte einer Matrix berechnen?
Das Programm bewirkt die Lösung eines linearen Gleichungssystems.
Mit einer symmetrischen Matrix 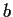 kann man auch Eigenwerte und Eigenvektoren
berechnen:
kann man auch Eigenwerte und Eigenvektoren
berechnen:
MATRIX.
COMPUTE b={2,10,3,5;10,15,12,4;3,12,5,4;5,4,4,5}.
PRINT b.
CALL EIGEN(b,evec,ewerte) .
PRINT evec.
PRINT ewerte.
END MATRIX.
3.]
Die Restlebenszeit 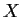 einer Person sei eine
Zufallsgröße. Es sei bekannt, daß
einer Person sei eine
Zufallsgröße. Es sei bekannt, daß
a) Berechnen Sie die Dichte und den Erwartungswert von 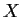 .
.
b) Konstruieren Sie mit Hilfe der Momentenmethode eine Schätzung für
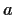 .
.
c)
Unter Verwendung der Verteilungsfunktion von 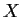 kann man mit der
Inversionsmethode Zufallszahlen erzeugen, die die Verteilung von
kann man mit der
Inversionsmethode Zufallszahlen erzeugen, die die Verteilung von 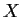 simulieren.
Bestimmen Sie damit mit SPSS die Schätzung
simulieren.
Bestimmen Sie damit mit SPSS die Schätzung
für 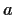 auf Grund einer Stichprobe vom Umfang
auf Grund einer Stichprobe vom Umfang 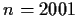 .
.
a) Es ist
also die Dichte
Der Erwartungswert ist dann
b) Verwendet man diese Resultat, kann man als Schätzung für 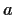 die
Gleichung herumdrehen:
die
Gleichung herumdrehen:
c) Wir konstruieren eine Verteilung für 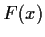 . Sei z.B.
. Sei z.B. 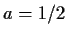 gewählt. Zur Anwendung der Inversionsmethode bestimmen wir noch die
Umkehrfunktion von
gewählt. Zur Anwendung der Inversionsmethode bestimmen wir noch die
Umkehrfunktion von
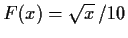 zu
zu
Berechnet man für die gefragten 2001 Zufallswerte vorerst
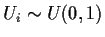 ,
d.h. gemäß einer Gleichverteilung, dann sind die Zahlen
,
d.h. gemäß einer Gleichverteilung, dann sind die Zahlen
die gesuchten Zufallszahlen mit der Verteilung 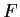 . Im SPSS-Test ergab
sich bei n=100:
. Im SPSS-Test ergab
sich bei n=100: 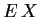 =32.54, und bei n=2001:
=32.54, und bei n=2001: 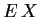 =32.5524 (statt des
theoretischen 100/3),
somit ist die Schätzung
=32.5524 (statt des
theoretischen 100/3),
somit ist die Schätzung 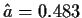 .
Mittels eines Histogrammes kann man sich diese Werte veranschaulichen.
Es sollte sich ein analoges Bild ergeben, wenn man
.
Mittels eines Histogrammes kann man sich diese Werte veranschaulichen.
Es sollte sich ein analoges Bild ergeben, wenn man
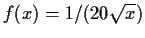 direkt über einer
Achse von (0,100) zeichnet.
direkt über einer
Achse von (0,100) zeichnet.
Dr.Wolfgang Quapp
2001-12-19
![]() -verteilt sind mit unbekannten
-verteilt sind mit unbekannten ![]() und
und ![]() .
Es ergaben sich für eine Stichprobe vom Umfang
.
Es ergaben sich für eine Stichprobe vom Umfang ![]() folgende Gewichte (in
kg):
folgende Gewichte (in
kg):
![]() für
für ![]() zum
Niveau
zum
Niveau ![]() .
.
![]() -Test
-Test
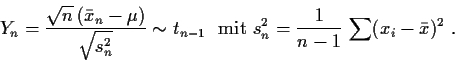
![]() kann man auch Eigenwerte und Eigenvektoren
berechnen:
kann man auch Eigenwerte und Eigenvektoren
berechnen:
![]() einer Person sei eine
Zufallsgröße. Es sei bekannt, daß
einer Person sei eine
Zufallsgröße. Es sei bekannt, daß