Dr.Quapp: Statistik für Mathematiker mit SPSS
11. Übung - Stichproben, Matrizen, Restlebenszeit -
- 1.
- Für die Gewichte von Warenpackungen wird angenommen, dass sie
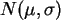 -verteilt sind mit unbekannten
-verteilt sind mit unbekannten 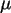 und
und 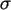 .
Es ergaben sich für eine Stichprobe vom Umfang
.
Es ergaben sich für eine Stichprobe vom Umfang 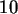 folgende Gewichte (in
kg):
folgende Gewichte (in
kg):
20,40,
20,25
20,00,
19,80,
20,05,
19,90,
20,50,
20,15,
20,20,
20,10.
Man bestimme ein Schätzintervall der Form  für
für 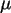 zum
Niveau
zum
Niveau 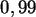 .
.
- 2.
- Geben Sie folgendes Syntax-Programm in SPSS ein .
MATRIX.
COMPUTE a={2,10,3,5;1,15,2,4;3,12,5,3;2,20,4,5}.
PRINT a.
COMPUTE c={1180;1001;1507;1574}.
Print c.
COMPUTE x=INV(a)*c.
PRINT x.
compute y=a*x.
Print y .
END MATRIX.
Was bewirkt das Programm?
- 3.
- Die Restlebenszeit
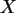 einer Person sei eine
Zufallsgröße. Es sei bekannt, daß
einer Person sei eine
Zufallsgröße. Es sei bekannt, daß
a) Berechnen Sie die Dichte und den Erwartungswert von 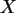 .
.
b) Konstruieren Sie mit Hilfe der Momentenmethode eine Schätzung für
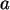 .
.
c)
Unter Verwendung der Verteilungsfunktion von 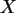 kann man mit der
Inversionsmethode Zufallszahlen erzeugen, die die Verteilung von
kann man mit der
Inversionsmethode Zufallszahlen erzeugen, die die Verteilung von 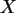 simulieren.
Bestimmen Sie damit mit SPSS die Schätzung
simulieren.
Bestimmen Sie damit mit SPSS die Schätzung
für 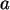 auf Grund einer Stichprobe vom Umfang
auf Grund einer Stichprobe vom Umfang 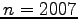 .
.
(Mit diesem 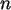 verabschieden wir uns nächste Woche aus diesem Jahr! Alles Gute für
verabschieden wir uns nächste Woche aus diesem Jahr! Alles Gute für
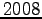 .)
.)
Quapp
2007-12-06