Dr.Quapp: Statistik für Mathematiker mit SPSS

Hinweise zur 10. Übung - Stichproben -

1.] a) Ein Massenartikel ( N$>$15000 ) habe eine NORMAL-verteilte Ausschußrate von p=10% (Nullhypothese).
Eine Stichprobe von n=100 soll diese Nullhypothese überprüfen. Berechnen Sie zum Signifikationsniveau $\alpha$=0,05 den kritischen Wert der Testgröße für n.
Anleitung: Im Intervall von 0 bis 1/3 für p$_0$ für ein p(i) mit i=1,...,301 Werten die Dichte der Normalverteilung direkt berechnen; und diese bis zum kritischen Wert 0,95 aufsummieren.
Für die Varianz gilt näherungsweise $\sigma^2$=p$_0$ (1-p$_0$) /n, da erfüllt ist: n/N$<$0,05.
Skalieren Sie noch probeweise den p-Bereich auf Standardwerte z.

Die Aufgabe soll die typische Situation einer Stichprobe nachspielen. Bei hinreichend großem $n$ kann man davon ausgehen, daß der Mittelwert der Stichprobe normalverteilt ist. Dies ist unabhängig davon, wie die ursprüngliche Verteilung der N Daten war.
Das Intervall ergibt sich mit 301 Zeilen zu p=($casenum-1)/900 . Man setze somit den Ausschuß-Anteil in einer Stichprobe als Normalverteilung mit $p_0=0.1$ an. Dies ist die Nullhypothese H$_o$. Da wir je definierte Stichproben betrachten, ist die Varianz wie in der Aufgabe angegeben $\sigma_0^2$=0.1 (1-0.1)/100=0.0009, also $\sigma_0$=0.03. Die Formel rührt her von der Annahme, daß eine Binomialverteilung den Ausgang der Stichprobe leitet. Die Variable $nor1$ kann über dem Intervall direkt aus der Dichte der Normalverteilung berechnet werden.

$$nor1(p) = \frac{1}{0.03*\sqrt{2*3.14159}} \ e^{-\displaystyle\frac{(p - 0.1)^2}{0.0018}} \ ,$$

oder in SPSS direkt durch

$$nor1(p) = PDF.NORMAL(p, 0.1, 0.03) \ \ .$$

Entsprechend ergibt sich eine Approximation der Verteilungsfunktion als kumulatives Aufsummieren von $nor1$ im Fenster $\rightarrow$Transformieren, $\rightarrow$Zeitreihen, nach extra Anklicken der $\rightarrow$kumulativen Summe (!) und unter Beachtung der Intervall-Länge 1/900 der 300 Intervalle, oder mit CDF.NORMAL(p, 0.1, 0.03). Der gesuchte kritische Wert des Tests ist der Wert 0.95 der Verteilungsfunktion, also die Stelle wo 95% überschritten wird: Bei p$_{krit}$=0.149 in Zeile 134. (Danach beginnt der $\alpha$-Fehler, wenn die Nullhypothese richtig war: Sollten in der Stichprobe doch zufällig mehr schlechte Teile sein.) Für eine Stichprobe mit n=100 heißt das, daß bis zu 14 Fälle Ausschuß toleriert werden, aber eine Stichprobe mit größer gleich 15 Fällen Ausschuß zurückgewiesen werden muß.

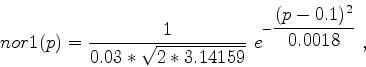
b) Die Alternativ-Hypothese der Ausschußrate sei p=20% .
Die Stichprobe von n=100 soll auch diese Hypothese überprüfen. Berechnen Sie zu (a) den entsprechenden $\beta$-Fehler.
Anleitung: Im Intervall von 0 bis 1/3 für p$_A$ für ein p(i) mit i=1,..., 300 Werte die Dichte der Normalverteilung mit p=0,2 direkt berechnen; und bis zum kritischen Wert von Aufgabe (a) aufsummieren. Für die Varianz gilt nun näherungsweise $\sigma^2$=p$_A$ (1-p$_A$) /n.

In b) soll nun noch der theoretisch denkbare Fall betrachtet werden, daß die Alternativhypothese exakt zu $p_A$=0.2 bekannt ist. Mit $\sigma_A^2$=0.2(1-0.2)/100=0.0016, also $\sigma_A$=0.04 ergibt sich eine Dichte $nor2$ analog zu oben; und die zugehörige Verteilungsfunktion. Dort kann man dann an der Stelle p$_{krit}$=0.149 der obigen kritischen Grenze einen Wert ablesen: 10.31 %. (Das ist dann der $\beta$-Fehler, wenn die Alternativhypothese gilt.)

c) Zeichnen Sie mit Hilfe von STREUPLOT die empirischen Dichten für p=0,1 und p=0,2 übereinander. Welches sind die Gebiete der $\alpha$- und $\beta$-Fehler? Mit SequencePlot sind diese schraffierbar.

Als $\rightarrow$Streudiagramm oder als $\rightarrow$Liniendiagramm - überlagert - über der Achse $p$ können beide Dichten gemeinsam in einer Abbildung gezeichnet werden. Graphisch können $\alpha$- und $\beta$-Fehler nur einzeln veranschaulicht werden, wenn man für $\rightarrow$SequenzDiagramm entsprechende Berandungs-Funktionen definiert:

$$\alpha = \left\{ \begin{array}{ll} nor1 & {\rm bei} p< ... ...888 \\ 0 & {\rm bei } p>0.14888 \\ \end{array} \right.$$

und

$$\beta = \left\{ \begin{array}{ll} 0 & {\rm bei} p< 0.14... ... nor2 & {\rm bei } p>0.14888 \\ \end{array} \right. .$$

Im SequenzDiagramm hat man dann entweder ($\alpha$ und $nor1$) oder ($\beta$ und $nor2$) zu verwenden, und im Format-Fenster ist je anzuklicken, daß ein Flächendiagramm verwendet werden soll, und die Variablen zu verbinden sind.
Die Bedeutung von $\alpha$ und $\beta$-Fehler bei einer Stichprobe entnimmt man der Tabelle:

H$_o$	H$_o$ nicht ablehnen	H$_o$ ablehnen	H$_A$
trifft zu	$\surd$	$\alpha$-Fehler	trifft nicht zu
trifft nicht zu	$\beta$-Fehler	$\surd$	trifft zu

Der $\alpha$-Fehler wird auch Fehler 1.Art genannt oder das Produzentenrisiko; der $\beta$-Fehler dann Fehler 2.Art oder das Konsumentenrisiko. Aus der Aufgabe sollte hervorgehen, daß man nicht beide Fehler gleichzeitig minimieren kann. Da Ablehnung von H$_o$ oder Annahme von H$_o$ vom kritischen Wert abhängt, den man aus der Verteilung von H$_o$ abliest, ist der Ausgang des Tests für $\beta$ also im allgemeinen Fall offen!

2] Ein Massenartikel ( N$>$15000 ) sei normalverteilt: Wir betrachten die Mast von Hähnchen. Der Mittelwert des Gewichtes sei $\mu$=492,5g bei einer Standardabweichung von $\sigma$=18,9g.
Mit einer Stichprobe von n=81 Tieren ergibt ein Fütterungsversuch mit einem anderen Futter das Resultat der Datei MASTHAHN.SAV.
Man kann annehmen, daß die Standardabweichung dabei nicht vom Futter abhängt. Kann man auf Grund des Stichproben-Versuches schließen, daß das neue Futter zu besseren Resultaten der Mast führt?
Die Antwort soll zu einem Signifikanzniveau $\alpha$=0.01 erfolgen.

Ist $\bar x$ der Mittelwert einer Stichprobe $n$, so nimmt man an, daß dieser um den wahren Mittelwert $\mu$ des Massenartikels $N$ schwankt.

$$E(\bar X) = E( \frac{1}{n} ( X_1 + ... + X_n)) = \frac{1}{n} ( E(X_1) + ... + E(X_n)) = \frac{1}{n} n E( X_1) = \mu .$$

Die Streuung des Massenartikels $\sigma$ geht dabei über in

$$Var(\bar X) = Var( \frac{1}{n} ( X_1 + ... + X_n)) = \fra... ...(X_n)) = \frac{1}{n^2} n Var( X_1) = \frac{\sigma ^2}{n} .$$

also hier zu $\sigma /\sqrt{n}$=18.9/9=2.1 für die Streuung von $\bar x$. Man kann dann für die Verteilung des Mittelwertes der Stichprobe die standardisierte Variable $Z$ betrachten mit

$$z= {\displaystyle \frac{\bar x -\mu }{\displaystyle \frac{\sigma}{\sqrt{n}}}} .$$

In einer Datenanalyse ergibt sich der Mittelwert der vorliegenden "Stichprobe", also des Fütterungstestes, zu 496.32, und wir verwenden das entsprechende $\sigma _n$=2.1. Die Verteilungsdichte für $Z$ ist eine Normalverteilung wie in Aufgabe 1, und die Grenze des kritischen Wertes kann im standardisierten Fall aus der Tabelle der Normalverteilung abgelesen werden: Bei $\alpha$=0.01 ist 99% des Anteils der Fläche der Dichte gefragt, also ist links vor der Fläche von 0.005, und rechts nach 0.995 abzuschneiden: $\Phi (z)$=0.995 ergibt z=2.5758 und $\Phi (z)$=0.005 ergibt z=-2.5758. Folglich ist das Konfidenz-Intervall für den Mittelwert theoretisch $\bar x \pm \sigma *$2.5758 also
99% CI Intervall = [ 490.92;501.73 ] .
Folgende Tabelle enthält die wichtigsten Quantile der Standard-Normalverteilung.

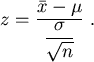
$\Phi (z)=\alpha$	0,75	0,9	0,95	0,975	0,99	0,995	0,9975	0,999
z	0,674	1,282	1,645	1,960	2,326	2,576	2,807	3,090

Dabei besteht noch die Symmetrie: $z_{1-\alpha}=-z_{\alpha}$.

In SPSS kann die Stichprobe auch mittels $\rightarrow$Analysieren, $\rightarrow$Explorative Datenanalyse betrachtet werden. Dabei kann zu den Daten der Mittelwert, und der Wert $\sigma /\sqrt{n}$ als der sogenannte Standardfehler berechnet werden. Weiterhin kann bei der $\rightarrow$Explorativen Datenanalyse im Feld $\rightarrow$Statistik ein Konfidenzintervall von 99% direkt eingestellt werden. Es ist der Standardfehler 0.267 und das 99% CI ist [490.88;501.77]. Die leichte Abweichung der Zahlen deutet darauf hin, daß $\sigma _n$ etwas verschoben ist, in der Tat ist in der Stichprobe $s$= 18.562. (Man beachte, daß in SPSS die sogenannte empirische Varianz $s^2$ mit dem Faktor 1/(n-1) verwendet wird.)
Obwohl der Fütterungsversuch mit einem anderen Futter einen etwas höheren Mittelwert der Gewichte der Hähnchen erbracht hat, kann diese Änderung noch nicht als signifikante Verschiebung des Mittelwertes betrachtet werden, da $\mu$ im CI liegt. Die Sache mit dem neuen Futter muß also noch weiter untersucht werden. Eine (im allgemeinen teure) Version der Weiterbetrachtung ist die Vergrößerung des Stichprobenumfanges $n$, womit natürlich $\sigma /\sqrt{n}$ kleiner wird.