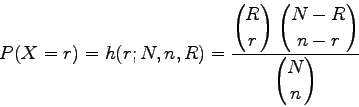Dr.Quapp: Statistik für Mathematiker mit SPSS
Hinweise zur 9. Übung - Kontingenztafel +
Likelihood-Schätzer
+ Zufallszahlen erzeugen
1.]
Die Verteilungsdichte eines 2-dimensionalen Zufallsvektor 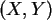 ist
folgendermaßen definiert:
ist
folgendermaßen definiert:
| P(X=x,Y=y) |
1 |
2 |
3 |
| 0 |
0,3 |
0,2 |
0,1 |
| 1 |
0,2 |
0,1 |
0,1 |
a) Denken Sie sich eine Datentabelle in SPSS aus, die dieser Kontingenztafel
entspricht. Bestimmen Sie die Randverteilungen von 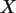 und
und 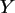 .
.
b) Berechnen Sie den Korrelationskoeffizienten von 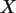 und
und 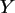 .
.
c) Bestimmen Sie die Verteilung, die Erwartung und die Varianz von 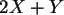 .
.
Die Aufgabe ist so reduziert, daß der theoretische Teil mit
Hand gelöst
werden kann. Dies sollte man auch einmal durchrechnen!
zu a) In SPSS erzeugt man eine Datentabelle mit 10 Zeilen und zwei Spalten für
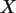 und
und 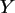 :
Sie enthält die Paare (0,1), (0,1), (0,1), (1,1), (1,1), (0,2), (0,2),
(1,2), (0,3) und (1,3).
:
Sie enthält die Paare (0,1), (0,1), (0,1), (1,1), (1,1), (0,2), (0,2),
(1,2), (0,3) und (1,3).
Will man sich, auch bei grösseren Problemen, das Aufzählen aller
einzelnen Fälle sparen, kann man mit Gewichten arbeiten:
Das Paar (0,1) zum Beispiel bekommt Gewicht 3, und dies muss in einem extra
Fenster  DatenWichten dann eingestellt werden.
Die 6 Paare haben Gewichte: 3,2,1,2,1,1.
Mit BeschreibenderStatistik, Kreuztabellen kann die gegebene Tabelle
erzeugt werden.
DatenWichten dann eingestellt werden.
Die 6 Paare haben Gewichte: 3,2,1,2,1,1.
Mit BeschreibenderStatistik, Kreuztabellen kann die gegebene Tabelle
erzeugt werden.
Die Randverteilungen sind entsprechende Zeilen- und
Spaltensummen; also 0.6 und 0.4 für 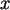 , sowie 0.5, 0.3, und 0.2 für
, sowie 0.5, 0.3, und 0.2 für
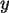 .
.
zu b)
Es ergibt sich: 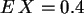 ,
,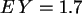 ,
und es ist:
,
und es ist:
![$Cov(X,Y)=E[(X-E X)(Y-E Y)]= E XY -E X E Y$](img10.png) mit
mit
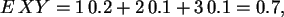 also
also
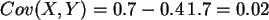
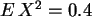 ,
,
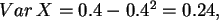
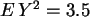 ,
,
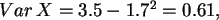
also
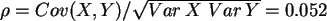 .
Dies bedeutet, daß
.
Dies bedeutet, daß 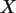 und
und 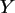 praktisch unabhängig sind. Aus den
Produkten der Randverteilung ergibt sich eine Tabelle mit
unabhängigen
praktisch unabhängig sind. Aus den
Produkten der Randverteilung ergibt sich eine Tabelle mit
unabhängigen 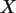 und
und 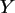 , vergleiche die Aufgabe:
, vergleiche die Aufgabe:
| P(X=x,Y=y) |
1 |
2 |
3 |
 |
| 0 |
0,3 |
0,18 |
0,12 |
0.6 |
| 1 |
0,2 |
0,12 |
0,08 |
0.4 |
 |
0.5 |
0.3 |
0.2 |
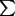 =1 =1 |
zu c)
Für 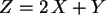 ergibt sich durch Ausrechnen die Tabelle:
ergibt sich durch Ausrechnen die Tabelle:
| z |
1 |
2 |
3 |
4 |
5 |
| P(Z=i) |
0.3 |
0.2 |
0.3 |
0.1 |
0.1 |
z |
1 |
4 |
9 |
16 |
25 |
Also wird
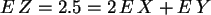 und
und 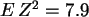 .
Damit dann die Varianz
.
Damit dann die Varianz
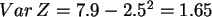 .
Man beachte wieder, daß SPSS die "empirischen" Varianzen berechnet:
.
Man beachte wieder, daß SPSS die "empirischen" Varianzen berechnet:
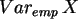 =0.26,
=0.26,  =0.68,
=0.68, 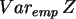 =1.83.
Zum Vergleich muß man
diese mit (n-1)/n=0.9 multiplizieren. Siehe auch Befehle in spss091.sps.
=1.83.
Zum Vergleich muß man
diese mit (n-1)/n=0.9 multiplizieren. Siehe auch Befehle in spss091.sps.
2.]
Erzeugen Sie in Form einer Tabelle zur hypergeometrischen Verteilung
h(r,N,n,R) mit N=13 und n=6 die Wahrscheinlichkeitsdichten h(r ,N,n,R
,N,n,R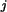 )
für r
)
für r aus dem Intervall [0,6] und R
aus dem Intervall [0,6] und R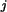 aus dem Intervall [1,13].
Deuten Sie Zeilen und Spalten dieser Tabelle als Wahrscheinlichkeitsdichten
bzw.als Likelihood-Funktion.
aus dem Intervall [1,13].
Deuten Sie Zeilen und Spalten dieser Tabelle als Wahrscheinlichkeitsdichten
bzw.als Likelihood-Funktion.
Überlegen Sie sich Konfidenzintervalle entsprechender Likelihood-
Schätzer zum Niveau 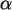 =0.1 .
=0.1 .
Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeiten beim
Urnenmodell ohne Zurücklegen. Es seien
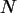 die Anzahl der Kugeln,
die Anzahl der Kugeln,
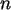 eine Stichprobe,
eine Stichprobe,
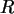 die Anzahl der roten Kugeln in
die Anzahl der roten Kugeln in 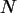 , und
, und
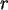 die roten Kugeln in der Stichprobe. Dann gibt
die roten Kugeln in der Stichprobe. Dann gibt
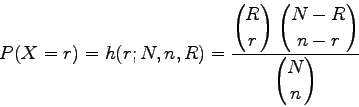
als Funktion von 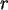 mit den Parametern
mit den Parametern 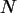 ,
, 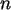 ,
, 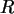 die Wahrscheinlichkeit an, daß genau r rote Kugeln in der Stichprobe
sind.
Die Verteilungsfunktion wird kumulativ
die Wahrscheinlichkeit an, daß genau r rote Kugeln in der Stichprobe
sind.
Die Verteilungsfunktion wird kumulativ
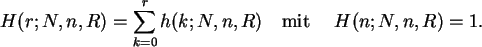
Im Parameter 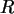 ist
ist 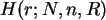 monoton fallend.
monoton fallend.
Ein Schätzproblem besteht darin, aus einer Stichprobe zurück auf 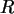 zu schätzen. Die Maximum-Likelihood-Idee sucht dabei jenen
Parameterwert, für den das beobachtete Testresultat am wahrscheinlichsten
ist. (Bei einer bekannten Art der Verteilungsdichte ist "nur" der
zugehörige Parameter gesucht.)
Sei bei einer Realisierung der Stichprobe für ein festes
zu schätzen. Die Maximum-Likelihood-Idee sucht dabei jenen
Parameterwert, für den das beobachtete Testresultat am wahrscheinlichsten
ist. (Bei einer bekannten Art der Verteilungsdichte ist "nur" der
zugehörige Parameter gesucht.)
Sei bei einer Realisierung der Stichprobe für ein festes 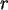 die
Parameterfunktion dann
die
Parameterfunktion dann
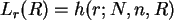 - bei festem
- bei festem 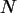 und
und 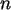 .
Wir suchen den Maximum-Likelihood-Schätzer
.
Wir suchen den Maximum-Likelihood-Schätzer
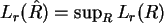 . Für
. Für 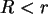 ist
ist 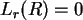 .
Wir betrachten den Quotient für zwei aufeinanderfolgende
.
Wir betrachten den Quotient für zwei aufeinanderfolgende 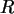 -Werte:
-Werte:
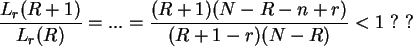
Die Kleinerrelation ist für
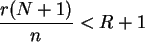
erfüllt. Also ist die Grenze
![$\hat R = \left[ \frac{ r (N+1) }{ n } \right] $](img43.png) . Davor gilt die
Ungleichung nicht, bei
. Davor gilt die
Ungleichung nicht, bei 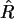 ist das Maximum überschritten.
ist das Maximum überschritten.
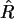 ist der Maximum-Likelihood-Schätzer für
ist der Maximum-Likelihood-Schätzer für 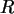 auf Grund des
gefundenen
auf Grund des
gefundenen 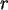 .
Im Grenzfall
.
Im Grenzfall 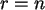 folgt
folgt 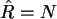 was nicht unlogisch ist, und wenn
was nicht unlogisch ist, und wenn
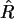 ganzzahlig ist, so ist auch noch
ganzzahlig ist, so ist auch noch
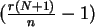 ein Schätzer.
ein Schätzer.
Sei nun N=13 und n=6. In SPSS können dann 7 Zeilen für  von 0 bis 6
belegt werden, und dazu sind dann 13 Variable Hy
von 0 bis 6
belegt werden, und dazu sind dann 13 Variable Hy in 13 Spalten einzeln
berechenbar:
in 13 Spalten einzeln
berechenbar:
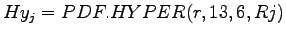 mit je
mit je 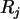 =1,2,...,13 mit der Dichte der
hypergeometrischen Verteilung
von SPSS.
(In SPSS ist die Variable
=1,2,...,13 mit der Dichte der
hypergeometrischen Verteilung
von SPSS.
(In SPSS ist die Variable 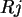 etwas schräg als ''Treffer'' bezeichnet.)
Der Vollständigkeit halber sollte noch eine Hy
etwas schräg als ''Treffer'' bezeichnet.)
Der Vollständigkeit halber sollte noch eine Hy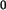 -Spalte eingefügt werden:
Wenn
-Spalte eingefügt werden:
Wenn 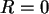 , dann ist sicher auch
, dann ist sicher auch 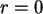 , also steht in der ersten Zeile dort eine 1,
sonst Nullen.
Die Zeilen dieser Hy-Tabelle ergeben die Likelihood-Funktion zu einer
Realisierung der Stichprobe für
, also steht in der ersten Zeile dort eine 1,
sonst Nullen.
Die Zeilen dieser Hy-Tabelle ergeben die Likelihood-Funktion zu einer
Realisierung der Stichprobe für 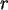 .
.
Durch einen Syntax-Zyklus ist die Rechnung wieder zu vereinfachen:
/* Ein ZyklusHypergeometricus fuer Zahlen R_j in (1,13) */
Input Program .
LOOP #I=1 to 7 .
Compute r=#I -1 .
Compute Rgr=1 .
DO REPEAT
B=Hy1 to Hy13 .
COMPUTE B= PDF.HYPER(r,13,6,Rgr) .
Compute Rgr=Rgr+1 .
END REPEAT .
END CASE .
END LOOP .
END FILE .
END INPUT PROGRAM .
EXECUTE .
/* Hy_i: Tabelle der Dichten der Hypergeometrischen Verteilung fuer N=13, n=6 */
/* Die Zeilen sind fuer r, die Spalten fuer R */
Zu Konfidenzbereichen:
Betrachtet man eine Spalte der Tabelle für einen festen
Wert von 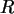 , so ist die Summe der
Wahrscheinlichkeiten über P(R=r) Eins (wie zu erwarten war).
Die Zeilen dagegen bilden die jeweilige Likelihood-Funktion.
Bei
, so ist die Summe der
Wahrscheinlichkeiten über P(R=r) Eins (wie zu erwarten war).
Die Zeilen dagegen bilden die jeweilige Likelihood-Funktion.
Bei 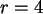 etwa hat diese ihr Maximum bei
etwa hat diese ihr Maximum bei 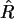 =9, dies ist somit der
Maximum-Likelihood-Schätzer für
=9, dies ist somit der
Maximum-Likelihood-Schätzer für 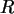 , was auch aus obiger Formel
herauskommt! Bei gegebenem
, was auch aus obiger Formel
herauskommt! Bei gegebenem 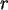 kann man natürlich nicht mit 100%-iger Sicherheit
auf ein
kann man natürlich nicht mit 100%-iger Sicherheit
auf ein 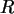 schließen, nur
schließen, nur
 ist sicher.
Grenzt man aber
die ''Sicherheit'' ein auf einen Wert 1-
ist sicher.
Grenzt man aber
die ''Sicherheit'' ein auf einen Wert 1-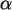 , so kann man grob gesprochen
den kumulativen Bereich der
entsprechenden Wahrscheinlichkeiten ablesen, wenn man die Zeilen noch
''normiert''.
Bei
, so kann man grob gesprochen
den kumulativen Bereich der
entsprechenden Wahrscheinlichkeiten ablesen, wenn man die Zeilen noch
''normiert''.
Bei 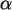 =0.1 bleibt die Rest-Summe 0.9 übrig,
und bei
=0.1 bleibt die Rest-Summe 0.9 übrig,
und bei 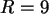 etwa sind das die Fälle für
etwa sind das die Fälle für 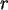 =3, 4, 5.
Betrachtet man nun ein erhaltenes
=3, 4, 5.
Betrachtet man nun ein erhaltenes 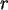 , so kann man diese R-Intvalle
abzählen.
Das Resultat
, so kann man diese R-Intvalle
abzählen.
Das Resultat 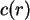 sind die folgenden Intervalle für
sind die folgenden Intervalle für 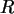 .
.
| r |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
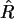 |
0 |
2 |
4 |
6, 7 |
9 |
11 |
13 |
| c(r) |
0-3 |
1-6 |
2-8 |
4-9 |
5-11 |
7-12 |
10-13 |
Es ist klar, daß der Schätzer im Konfidenzintervall liegt.
3.]
Zur Erzeugung gleichmäßig in 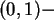 verteilter Zufallszahlen
benutzt man häufig lineare Kongruenzen: Zunächst werden
Zufallszahlen über der Menge {0, 1, 2, ... ,m} gemäß
verteilter Zufallszahlen
benutzt man häufig lineare Kongruenzen: Zunächst werden
Zufallszahlen über der Menge {0, 1, 2, ... ,m} gemäß
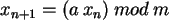 erzeugt, wobei
erzeugt, wobei 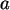 eine ganze Zahlen ist. Dann
sind
eine ganze Zahlen ist. Dann
sind
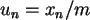 Zufallszahlen aus
Zufallszahlen aus 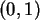 .
Erzeugen Sie mit dieser Vorschrift
.
Erzeugen Sie mit dieser Vorschrift 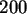 Zufallszahlen mit
Zufallszahlen mit 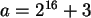 und
und
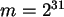 . Analysieren Sie die Daten durch Vergleich mit Zufallszahlen von
SPSS. (Variieren Sie auch
. Analysieren Sie die Daten durch Vergleich mit Zufallszahlen von
SPSS. (Variieren Sie auch 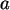 und
und 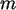 ! )
! )
Folgendes SPSS-Programm löst die Aufgabe
( Syntax-Datei in D: spss093.sps ):
/* Berechnung von Zufallszahlen aus (0,1) */
/* Ein erstes Feld im Datenfenster muss aktiviert sein */
/* Startwerte */
COMPUTE y=100000.
COMPUTE A=2**16 +3.
COMPUTE m=2**31.
EXECUTE.
/* Ein Zyklus fuer Zahlen in (0,1) */
/* Die Hilfsvariable Y liegt dabei in (0,m) */
Do Repeat
B=x1 to x200.
COMPUTE Y=MOD(Y*A,m).
COMPUTE B=Y/m.
END REPEAT.
EXECUTE.
/* Transponieren der berechneten Zeile in eine Spalte,
die neue Variable dieser Spalte wird var001 */
FLIP Variables= x1 to x200 .
/* Berechne Vergleichsvariable uu */
COMPUTE
uu=RV.UNIFORM(0,1) .
EXECUTE.
GRAPH
/HISTOGRAM=var001 .
GRAPH
/HISTOGRAM=uu .
EXECUTE.
Die Histogramme sind im Allgemeinen vom SPSS-Programm mit verschieden-anzahligen
Balken berechnet, so daß die Bilder nicht direkt vergleichbar sind.
Dies kann man mit Hand verstellen.
Aber unsere Zufallszahlen liegen sozusagen theoretisch gut im Trend:
Der Mittelwert war bei einem Test mit 0.49 sogar besser als der von SPSS mit 0.47.
Es ist ja
 , wenn
, wenn 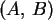 das Intervall
ist, und
das Intervall
ist, und
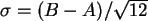 , also hier 0.2887.
Die Streuung von
, also hier 0.2887.
Die Streuung von 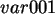 ist 0.28, die von
ist 0.28, die von 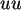 0.29; also beides sehr ordentliche Werte.
0.29; also beides sehr ordentliche Werte.
Quapp 2007-12-06