Dr.Quapp: Statistik für Mathematiker mit SPSS
9. Übung - Kontingenztafel +
Likelihood-Schätzer + Zufallszahlen erzeugen
- 1.
- Die Verteilungsdichte eines 2-dimensionalen Zufallsvektor
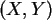 ist
folgendermaßen definiert:
ist
folgendermaßen definiert:
a) Denken Sie sich eine Datentabelle in SPSS aus, die dieser Kontingenztafel
entspricht. Bestimmen Sie die Randverteilungen von 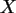 und
und 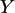 .
.
b) Berechnen Sie den Korrelationskoeffizienten von 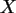 und
und 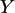 .
.
c) Bestimmen Sie die Verteilung, die Erwartung und die Varianz von 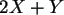 .
.
- 2.
- Erzeugen Sie in Form einer Tabelle zur hypergeometrischen Verteilung
h(r,N,n,R) mit N=13 und n=6 die Wahrscheinlichkeitsdichten h(r
 ,N,n,R
,N,n,R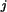 )
für r
)
für r aus dem Intervall [0,6] und R
aus dem Intervall [0,6] und R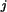 aus dem Intervall [1,13].
Deuten Sie Zeilen und Spalten dieser Tabelle als Wahrscheinlichkeitsdichten
bzw.als Likelihood-Funktion.
aus dem Intervall [1,13].
Deuten Sie Zeilen und Spalten dieser Tabelle als Wahrscheinlichkeitsdichten
bzw.als Likelihood-Funktion.
Überlegen Sie sich Konfidenzintervalle entsprechender Likelihood-
Schätzer zum Niveau 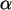 =0.1 .
=0.1 .
- 3.
- Zur Erzeugung gleichmäßig in
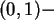 verteilter Zufallszahlen
benutzt man häufig lineare Kongruenzen: Zunächst werden
Zufallszahlen über der Menge {0, 1, 2, ... ,m} gemäß
verteilter Zufallszahlen
benutzt man häufig lineare Kongruenzen: Zunächst werden
Zufallszahlen über der Menge {0, 1, 2, ... ,m} gemäß
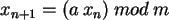 erzeugt, wobei
erzeugt, wobei 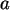 eine ganze Zahlen ist. Dann
sind
eine ganze Zahlen ist. Dann
sind
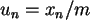 Zufallszahlen aus
Zufallszahlen aus 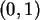 .
Erzeugen Sie mit dieser Vorschrift
.
Erzeugen Sie mit dieser Vorschrift 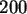 Zufallszahlen mit
Zufallszahlen mit 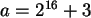 und
und
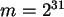 . Analysieren Sie die Daten durch Vergleich mit Zufallszahlen von
SPSS. (Variieren Sie auch
. Analysieren Sie die Daten durch Vergleich mit Zufallszahlen von
SPSS. (Variieren Sie auch 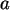 und
und 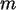 ! )
! )
Dr.Wolfgang Quapp
2004-11-30
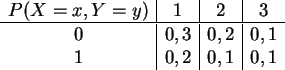
![]() =0.1 .
=0.1 .