Dr.Quapp: Statistik für Mathematiker mit SPSS

Hinweise zur 8. Übung - - Faltung + Grenzwertsatz von Moivre-Laplace

[1.] Erzeugen Sie (je 200 Zeilen) von zwei diskreten Zufallsgrößen $X\sim BINOM(n_x,p)$, und $Y\sim BINOM(n_y,p)$ und bilden Sie damit die neuen Zufallsgröße $W=X+Y$. Überprüfen Sie das bekannte Faltungsverhalten der Binomialverteilung, d.h. berechnen Sie die resultierenden Parameter $n_w$ und $p_w$.

Aus einem Bernoulli-Experiment B$_1$ mit Ja-Nein Entscheidung mit Wahrscheinlichkeit p zu (1-p) entsteht durch Wiederholung, d.h. durch Addition der Zufallsvariablen B$_1$ zu einer weiteren von gleichem Typ, die Binomialverteilung. Diese ist also per Definition schon eine Faltung.

$$BINOM(n,p) = \underbrace{ B_1(p) * B_1(p) * \cdots * B_1(p) }_{ \displaystyle{ n Faktoren }}$$

Dabei gilt die simple Relation 1=(p+(1-p))=(p+(1-p))$^n$ .
Folglich ist $BINOM(n,p) * BINOM(m,p) = BINOM(n+m,p)$
Sei im SPSS-Experiment $n_x$=10, $p$=1/3, und $n_y$=20. Wir benutzen den Mittelwert als Schätzer für $n_w$. Es ergab sich für die Mittelwerte: M$_x$=3.36, M$_y$=6.665 und für die Summe beider Zufallsvariablen M$_w$=10.025, was $n_w$=30 entspricht. Aus Mittelwert und Varianz kann man auch wieder $p$ schätzen: M/Var=(1-p), hier ergab sich $(1-p_w)$=0.64.

[2.] Erzeugen Sie (je 200 Zeilen) von zwei diskreten Zufallsgrößen $X, Y \sim POISSON(\lambda _x)$, $POISSON(\lambda _y)$ und bilden Sie damit die neuen Zufallsgrößen $W = X + Y .$ Überprüfen Sie das bekannte Faltungsverhalten der Poissonverteilung, d.h. berechnen Sie den resultierenden Parameter $\lambda _w$ für ein $w=POISSON(\lambda _w, k)$.

Die Dichte der Poissonverteilung an der Stelle $l$ ist

$$d(\lambda )(l) = e^{-\lambda } \frac{\lambda ^l}{l!}$$

Die Faltung ist also direkt

$$d(\lambda _x) * d(\lambda _y)(k) = \sum_{l=0}^{k} e^{-\lamb... ... \sum_{l=0}^{k} {k \choose l} \lambda _x^l \lambda _y^{k-l} =$$

$$=e^{-(\lambda _x +\lambda _y )} \frac{(\lambda _x +\lambda _y )^k}{k!} = d(\lambda _x + \lambda _y)(k) .$$

Sei im SPSS-Experiment $\lambda _x$=5 und $\lambda _y$=10. Wir benutzen den Mittelwert als Schätzer für $n_w$. Es ergab sich für die Mittelwerte: M$_x$=5.205, M$_y$=9.745 und für die Summe beider Zufallsvariablen M$_w$=14.95, was $\lambda _w$=15 entspricht. Einfacher ist noch die Betrachtung der Modalwerte als Schätzer für $n_w$: 5+10=15.

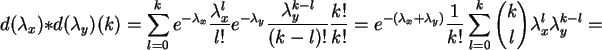
[3.] Erzeugen Sie (je 200 Zeilen) von zwei Zufallsgrößen $X, Y \sim N(a_x,\sigma _x), N(a_y,\sigma _y)$ und bilden Sie damit neue Zufallsgrößen $W=X+Y$ und $V=X-Y$. Überprüfen Sie das bekannte Faltungsverhalten der Normalverteilung, d.h. berechnen Sie die resultierenden Mittelwerte und Streuungen von $W$ und $V$.

Für die Normalverteilung gilt bekannterweise

$$N(a_x,\sigma _x) * N(a_y,\sigma _y) = N(a_x + a_y , \sqrt{ \sigma _x^2 + \sigma _y^2})$$

Sei im SPSS-Experiment $a_x$=1, $a_y$=2, $\sigma _x$=2, und $\sigma _y$=5. Es ergab sich für die Mittelwerte: M$_x$=1.078, M$_y$=2.064 und für die Summe beider Zufallsvariablen exakt M$_w$=3.142 und die Differenz M$_v$=-0.986. Die Varianzen ergaben sich zu Var$_x$=2.13, Var$_y$=4.92 und für die Summe beider Zufallsvariablen Var$_w$=5.345, bzw. Var$_v$=5.372, was $\sqrt{ 2.13^2 + 4.92^2}$=5.361 gut entspricht.

[4.] Erzeugen Sie (je 200 Zeilen) von zwei Zufallsgrößen $X\sim CHISQ(df_x)$, und $Y\sim CHISQ(df_y)$ und bilden Sie damit die neuen Zufallsgrößen $W = X + Y .$ Überprüfen Sie das bekannte Faltungsverhalten der $\chi^2$-Verteilung, d.h. berechnen Sie den resultierenden Parameter $df_w$.

Für die $\chi^2$-Verteilung gilt analog wie in [1.], daß sie selbst schon eine Faltung ist:

$$CHISQ(n) = \underbrace{ \chi_1^2 * \chi_1^2 * \cdots * \chi_... ... Faktoren }} \ ( = \Gamma _{\frac{1}{2},\frac{n}{2}} )$$

Folglich addieren sich wieder die Parameter $df_x$ und $df_y$ .
Sei im SPSS-Experiment $df_x$=5 und $df_y$=15. Wir benutzen den Mittelwert als Schätzer für $df_w$. Es ergab sich für die Mittelwerte: M$_x$=5.36, M$_y$=14.44 und für die Summe beider Zufallsvariablen M$_w$=19.80, was $df_w$=20 ergibt. Die Varianz wäre ein etwas schlechterer Schätzer für $df_w$: Es ergab sich für: Var$_x$=9.12, Var$_y$=24.41 und für die Summe beider Zufallsvariablen Var$_w$=33.69, was $df_w$=17 entspräche.

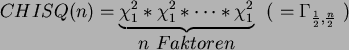
[5.] Die Binomialverteilung $BINOM(n,p)$ läßt sich durch die Normalverteilung approximieren, wenn $p$ nicht zu nahe an 0 oder 1 ist, und wenn $n$ hinreichend groß ist (zentraler Grenzwertsatz). Vergleichen Sie mit $\rightarrow$Streu-Diagramm die Verteilungsfunktionen von N(0,1) und der entsprechend verschobenen Verteilungsfunktion der Binomialverteilung für $p$=1/3 und $n$=10, 30, 100, und 300.
Hinweis: "verschoben" bedeute, wenn $B\sim BINOM(n,p)$ ist, dann sollte $(B-np)/\sqrt{np(1-p)}$ näherungsweise nach $N(0,1)$ verteilt sein. In SPSS kann damit die Binomialverteilung auf einer ganzzahligen Achsenvariablen $x$ ( mit $B_n$=CDF.BINOM(x,n,1/3) ) verschoben werden zu der neuen Achsenvariablen $x_n$ durch $x_n=(x-np)/\sqrt{np(1-p)}$. Mit dieser sind je zwei Verteilungen $B_n$ und $N(0,1)$ gleichzeitig betrachtbar. Die 4 Fälle für $x_n$ sind einzeln zu behandeln.
Für np(1-p)$\ge$9 ist das Ersetzen der Binomialverteilung durch die Normalverteilung mit np $\rightarrow \mu$ und np(1-p) $\rightarrow \sigma ^2$ möglich. Also bei p=1/3 ab n$>$40. Mit den Befehlen aus spss085V12.sps kann die Aufgabe in einem Syntaxfenster abgearbeitet werden. Ein Feld muss dabei im Datenfenster aktiviert sein.