Dr.Quapp: Statistik für Mathematiker mit SPSS
6. Übung - Spezielle Verteilungen
- 1.
a) Erzeugen Sie (je 200 Zeilen) von 10
Zufallsgrößen
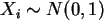 mit i=1,...,10; und bilden Sie damit
die neue Zufallsgröße
mit i=1,...,10; und bilden Sie damit
die neue Zufallsgröße
b)
Erzeugen Sie eine weitere Zufallsvariable  (ebenfalls 200
Ausprägungen) nach der
(ebenfalls 200
Ausprägungen) nach der 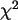 -Verteilung mit 10 Freiheitsgraden,
Hinweis: nutzen Sie RV.CHISQ(10), und vergleichen Sie
-Verteilung mit 10 Freiheitsgraden,
Hinweis: nutzen Sie RV.CHISQ(10), und vergleichen Sie 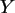 und
und  !
!
c) Erzeugen Sie zu einer Achsenvariablen ![$ A \in [0,30]$](img6.png) die Werte
der theoretischen Verteilungsfunktion der
die Werte
der theoretischen Verteilungsfunktion der 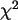 -Verteilung mit 10
Freiheitsgraden
-Verteilung mit 10
Freiheitsgraden 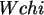 sowie die Werte der Dichtefunktion
sowie die Werte der Dichtefunktion 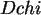 .
.
d) Bestimmen Sie Schiefe und Wölbung von 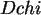 ! Hinweis: Die
Achsenvariable ist unter Verwendung der Dichte clever zu wichten!
! Hinweis: Die
Achsenvariable ist unter Verwendung der Dichte clever zu wichten!
- 2.
- a) Ausgehed von 50, 100 oder 200
Ausprägungen von zwei Zufallsvariablen
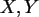 mit Normalverteilung
mit Normalverteilung
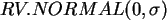 , z.B.
, z.B.
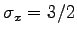 ,
, 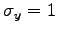 berechnen Sie die neue
Zufallsvariable
berechnen Sie die neue
Zufallsvariable
z.B. mit  .
.
b) Bestimmen Sie Mittelwert und Median von 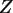 !
Kann man
!
Kann man 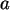 rückwärts aus statistischen
Kenngrößen von
rückwärts aus statistischen
Kenngrößen von 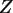 bestimmen?
bestimmen?
c) Vergleichen Sie damit eine Zufallsvariable
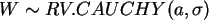 . Was ist der Erwartungswert
. Was ist der Erwartungswert 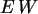 ?
?
d) Stellen Sie einen Zusammenhang her zur HCN-Aufgabe 4.2 !
Quapp
2007-11-16
![]() mit i=1,...,10; und bilden Sie damit
die neue Zufallsgröße
mit i=1,...,10; und bilden Sie damit
die neue Zufallsgröße