Dr.Quapp: Statistik für Mathematiker mit SPSS
5. Übung - Wiederholungen
- 1.
- Der Korrelationskoeffizient mißt die lineare Abhängigkeit von
zwei Zufallsgrößen. Nichtlineare Zusammenhänge kann man mit ihm
nicht erfassen.
a) Es sei 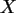 eine symmetrische Zufallsgröße und
eine symmetrische Zufallsgröße und 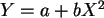 .
Zeigen Sie, dass
.
Zeigen Sie, dass 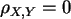 ist.
Wie sieht dann die beste Anpassung von
ist.
Wie sieht dann die beste Anpassung von 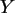 durch
durch
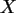 aus?
aus?
b) Es sei 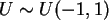 und
und 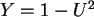 . Erzeugen Sie 100 Zufallszahlen
zu
. Erzeugen Sie 100 Zufallszahlen
zu 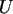 und
und 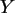 . Bestimmen Sie den
empirischen Korrelationskoeffizienten zwischen diesen Merkmalen und
danach die beste quadratische Anpassung.
. Bestimmen Sie den
empirischen Korrelationskoeffizienten zwischen diesen Merkmalen und
danach die beste quadratische Anpassung.
- 2.
- a) Erzeugen Sie mit Hilfe der Funktionen
RV.NORMAL(MW,
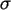 ) 100
nach N(0,1000) verteilte Zufallszahlen als Variable
) 100
nach N(0,1000) verteilte Zufallszahlen als Variable 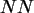 .
.
b) Erzeugen Sie die Variable Fallnummer (mit der Systemvariablen $casenum ).
c) Klassifizieren Sie die Variable 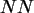 in 10 Klassen gleicher Breite
unter der Variablen
in 10 Klassen gleicher Breite
unter der Variablen 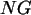 .
.
d) Berechnen und zeichnen Sie die empirischen
Verteilungsfunktionen von 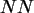 und
und 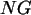 ,
und die "richtige" Verteilungsfunktion der Normalverteilung N(0,1000)
in einem gemeinsamen Bild,
und
bestimmen Sie den Abstand der Verteilungsfunktionen von
,
und die "richtige" Verteilungsfunktion der Normalverteilung N(0,1000)
in einem gemeinsamen Bild,
und
bestimmen Sie den Abstand der Verteilungsfunktionen von 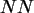 und N(0,1000).
und N(0,1000).
Hinweis: die Verteilungsfunktionen vieler Verteilungen stehen im Feld
 Berechnen unter der Abkürzung CDF.name(parameter) bereit.
Berechnen unter der Abkürzung CDF.name(parameter) bereit.
- 3.
- Erstellen Sie in SPSS die Variable ARGUMENT
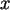 mit den Werten
mit den Werten
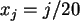 mit
mit
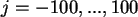 .
Zeichnen Sie den Graph der Funktionen
.
Zeichnen Sie den Graph der Funktionen 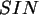 ,
, 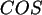 ,
, 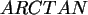 ,
, 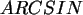 , und
, und
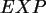 mit dem Grafikbefehl Streudiagramm.
mit dem Grafikbefehl Streudiagramm.
Dr.Wolfgang Quapp
2004-11-01