Dr.Quapp: Statistik für Mathematiker mit SPSS

Lösungs-Hinweise 2. Übung - Verteilungsfunktion

1. In zwei vierten Klassen (A und B) ergab eine Klassenarbeit die folgenden Zensuren:

Klasse A
Note	1	2	3	4	5	6
Anzahl	5	9	13	3	0	1

Klasse B
Note	1	2	3	4	5	6
Anzahl	3	6	10	2	1	2

a) Bestimmen Sie die empirischen Verteilungen $F_A$ und $F_B$ von beiden Zensurenspiegeln.

In drei Spalten sind die Werte der Tabelle einzutippen: Note, Anzahl$_A$, Anzahl$_B$. Mit
und
gibt es das richtige Fenster. Wir schieben die Variablen Anzahl$_A$ und Anzahl$_B$ ins obere rechte Fenster. Dies ergibt nach Ausführen neue Variablen Summe$_A$ und Summe$_B$, in der die Werte des Zensurenspiegels kumulativ aufaddiert sind.
Teilt man diese Variablen in durch den kumulativen Wert in der 6.Zeile: also bei A durch 31 und bei B durch 24, so ergeben sich die empirischen Verteilungsfunktionen $F_A$ und $F_B$.

b) Zeichnen Sie beide empirische Verteilungen $F_A$ und $F_B$ in einem Koordinatensystem.

Mit können die empirischen Verteilungsfunktionen beide dargestellt werden, indem noch

gewählt wird. Die Abszisse sollte der richtige Wert der Note sein. Also ist einzustellen: Werte einzelner Fälle, und im Fenster ist dann die Note für die Kategorienbeschriftung einzustellen.

c) Bestimmen Sie die Differenz der Verteilungsfunktionen

$$D:= max\ \{ \vert F_A(x) - F_B(x) \vert \ \ {\rm mit \ } -\infty <x < \infty \} .$$

Wir berechnen die neue Variable Di:

und Aufruf der Funktion ABS( ) im rechten Fenster: In die Klammern werden die Variablen $F_A - F_B$ geschoben. Das Maximum von Di kann bei 6 Werten leicht abgelesen werden; sind es mehr Fälle, so kann mit
in Statistik der Punkt Maximum der entsprechenden Variablen Di angeklickt werden. Es ergibt sich: D=0.093.

2. Gegeben sei die stetige Dichte $f(x)$ einer Zufallsvariablen X

$$f(x)= \left\{ \begin{array}{cc} -0.006 \ x^2 + 0.06 \ x \ , ... ...e 10 \\ 0 \quad \quad & {\rm sonst } \ . \end{array} \right.$$

a) Stellen Sie $f(x)$ und die Verteilungsfunktion $F(x)$ mittels SPSS graphisch dar.
Hinweis: Die Achsenvariable $x \in$[0.1,9.9] sei durch z.B. 99 "Fälle" equidistant representiert: Setze x=$casenum/10 im Fenster Transformieren. ($casenum ist eine Systemvariable.)

Zuerst muß dem SPSS-System mitgeteilt werden, wieviele "Fälle" zu bearbeiten sind. Dies geschieht am leichtesten durch Anklicken des Datenkästchens in der 1.Spalte, 99.Zeile. Danach kann die Variable x wie in der Aufgabe angegeben berechnet werden, und danach schon die Funktion f(x). Da außerhalb des Intervalls [0.1,9.9] der Funktionswert Null sein soll, ist keine Fallunterscheidung notwendig!
f(x) kann mit oder mit -$>$ Streudiagramm dargestellt werden (man verwende Werte einzelner Fälle (!) über x$_i$ ) .

Die Verteilungsfunktion F(x) ist die aufintegrierte Dichte:

$$F(x) = \int\limits_{-\infty}^{x} f(z) \ dz = \int\limits_{0}^{x} f(z) \ dz = -0.002\,x^3 + 0.03\,x^2$$

Dies kann man in SPSS näherungsweise durch eine Untersumme berechnen:

$$F(x_j) = \sum_{i=1}^{j} f(x_i) \ \Delta x_i$$

wobei die $\Delta x_i$ aus der Achsenteilung kommen, zu 0.1 . Im SPSS wird somit eine mit $\Delta x_i$=0.1 zu modifizierende kumulative Summe der Dichte f(x$_i$) berechnet. Damit ist die Verteilungsfunktion erstellt.
F(x) kann wieder mit oder mit -$>$ Streudiagramm dargestellt werden, oder beide Funktionen können gleichzeitig dargestellt werden.

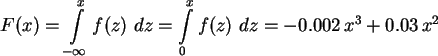
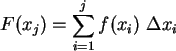
b) Berechnen Sie Erwartungswert $E(x)$ und Varianz $Var(x)$ direkt, als auch mit SPSS.

Es ist

$$E\,x = \int\limits_0^{10} x\,f(x)\,dx = \int\limits_0^{10} ... ...^3 + 0.06 x^2 ) \, dx = [ -0.0015 x^4 + 0.02 x^3 ]_0^{10} = 5$$

und

$$Var \, x = \int\limits_0^{10} x^2\,f(x)\,dx -(E \,x )^2 = \int\limits_0^{10} (-0.006 x^4 + 0.06 x^3 ) \, dx -25 =$$

$$\hspace*{1cm} =[ -0.0012 x^5 + 0.015 x^4 ]_0^{10} -25 = -120 +150 -25 = 5$$

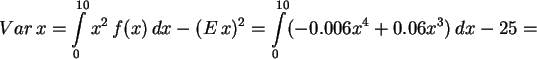
In SPSS sind die Integrale durch Untersummen anzupassen. Diese werden wieder durch kumulative Summen berechnet.

$$E\,x = \sum_1^{99} x_i \cdot f(x_i) \, \Delta x_i$$

und

$$Var \, x = \sum_1^{99} x_i^2 \cdot f(x_i) \, \Delta x_i - (E \,x )^2$$

Es ergibt sich (wie erwartet): Ex=5, Varx=5 , also $\sigma$ = 2.24.

Hinweis: Multipliziert man künstlich $f(x)$ z.B. mit 1000, so kann man auch wieder mit Gewichten arbeiten, siehe No2 von Übung1

Für diese Variante erzeugen wir aus f(x) eine neue Spalte "Gewichte", die größer als Eins sein sollen. Die Spalte f(x) kann mit etwa 1000 multipliziert werden.
Unter und
kann diese Variable als Gewicht für weitere Berechnungen verwendet werden. Dabei wird so verfahren, als ob jeder Wert der Realisierung (dies ist die Achsenvariable $x_i$) so oft auftritt, wie sein Gewicht angibt. In
schiebt man die Variable x in rechtes Fenster, und klickt in Mittelwert und Varianz an. Es ergibt sich analog: Ex=5, Varx=4.9985 .