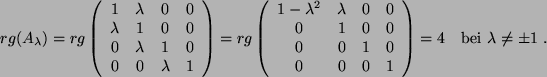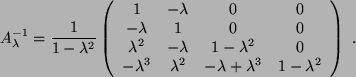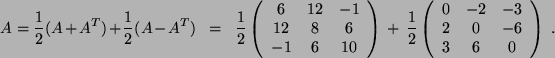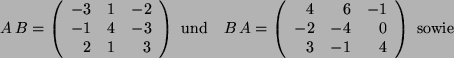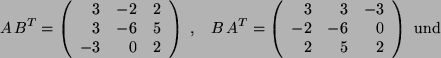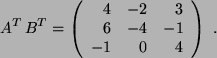- 38. a)
- Folgende (4,3) Matrix
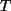 bildet die Basisvektoren von
bildet die Basisvektoren von 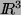 auf die
gegebenen Vektoren im
auf die
gegebenen Vektoren im 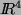 ab:
ab:
- b)
- Die lineare Abbildung
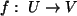 habe einen Kern
habe einen Kern 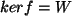 .
.
 ist ein Untervektorraum von
ist ein Untervektorraum von  .
Im Urbildraum
.
Im Urbildraum  kann man die Nebenklasse
kann man die Nebenklasse
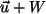 betrachten.
betrachten.
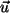 nennt man dann auch den Vertreter der Nebenklasse. Dies ist nicht
eindeutig!
nennt man dann auch den Vertreter der Nebenklasse. Dies ist nicht
eindeutig!
Es gelte nun zu diesem (beliebigen)
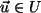 die Abbildung
die Abbildung
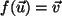 .
.
Beh.: Das Urbild von 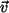 ist
ist
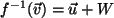 .
.
Bew.:
(i) Sei ein
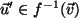 . Dann ist
. Dann ist
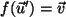 und wegen der Linearität ist
und wegen der Linearität ist
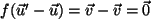 .
Also ist
.
Also ist
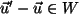 , oder anders geschrieben:
, oder anders geschrieben:
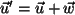 mit
mit
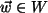 .
.
Das heisst
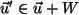 oder
oder
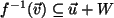 .
.
(ii) Sei nun 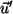 ein beliebiges Element aus der Menge der
Nebenklasse, d.h.
ein beliebiges Element aus der Menge der
Nebenklasse, d.h.
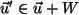 ,
d.h.es existiert ein
,
d.h.es existiert ein
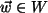 mit
mit
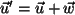 . Dann ist
. Dann ist
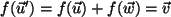 , also ist
, also ist
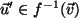 , und
, und
 . Kombiniert man (i) und (ii),
ergibt sich die Behauptung.
. Kombiniert man (i) und (ii),
ergibt sich die Behauptung.
Bemerkung:
Definiert man eine Äquivalenzrelation in 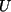 durch
durch
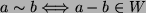 , so sind die Äquivalenzklassen
dieser Relation genau die Nebenklassen bezüglich
, so sind die Äquivalenzklassen
dieser Relation genau die Nebenklassen bezüglich 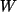 .
.
- c)
-
Die Linearität wird leicht nachgerechnet...
Der Kern bei einer Ableitung sind alle Konstanten.
Das Bild des Operators 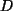 ist zu einem beliebigem Polynom
ist zu einem beliebigem Polynom
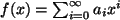 das
Polynom
das
Polynom
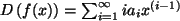 ,
also offenbar wieder alle denkbaren Elemente von V.
Somit ist
,
also offenbar wieder alle denkbaren Elemente von V.
Somit ist
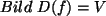 .
.
Obwohl es einen Kern gibt, hat das Bild die
gleiche Dimension wie das Urbild: unendlich.
- 39. a)
- Der Rang der Matrix ist
Dies ergibt sich leicht durch Spaltenoperationen:
Von hinten her wird die
 -te
Spalte durch
-te
Spalte durch
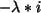 -te Spalte +
-te Spalte +  -te Spalte berechnet.
-te Spalte berechnet.
Die Inverse ist somit für
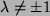 mit dem
Gauss-Jordan-Verfahren berechenbar, sie ist:
mit dem
Gauss-Jordan-Verfahren berechenbar, sie ist:
- 39. b)
- Der Rang von
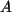 ist 4.
ist 4.
- 40. a)
- Es ist
und es ist
- b)
- Zu
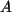 brauchen wir noch die transponierte Matrix
brauchen wir noch die transponierte Matrix 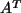 :
Die gesuchte Aufspaltung ergibt sich aus
:
Die gesuchte Aufspaltung ergibt sich aus
- c)
- Zu
ergibt sich:
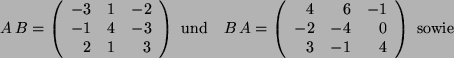
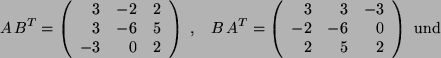
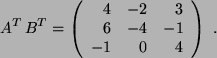
- 41.
- Ist
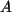 eine ganzzahlige quadratische Matrix, so ist auch die Determinante
von
eine ganzzahlige quadratische Matrix, so ist auch die Determinante
von 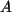 ganzzahlig - nach dem Determinantenentwicklungssatz.
ganzzahlig - nach dem Determinantenentwicklungssatz.
Wenn
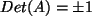 ist, so ergibt sich bei der Berechnung der Inversen
durch die komplementäre Matrix (
ist, so ergibt sich bei der Berechnung der Inversen
durch die komplementäre Matrix (
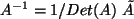 , und
, und
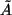 enthält nur ganzzahlige Unterdeterminanten)
wieder Ganzzahligkeit, dann sind wir fertig.
(Ein Beispiel war in Aufgabe 32 vorgekommen.)
enthält nur ganzzahlige Unterdeterminanten)
wieder Ganzzahligkeit, dann sind wir fertig.
(Ein Beispiel war in Aufgabe 32 vorgekommen.)
Wäre aber
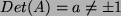 , so müsste
, so müsste
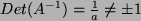 sein, also eine gebrochene
Rationalzahl.
Wäre nun aber
sein, also eine gebrochene
Rationalzahl.
Wäre nun aber 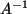 selbst trotzdem ganzzahlig,
dann müsste auch wieder die
Determinante von
selbst trotzdem ganzzahlig,
dann müsste auch wieder die
Determinante von 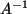 ganzzahling sein, wie oben.
Das ist ein Widerspruch.
ganzzahling sein, wie oben.
Das ist ein Widerspruch.
Dr.Wolfgang Quapp
2003-01-16