Sei
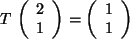 und
und
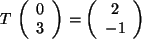 .
Ist
.
Ist
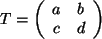 , so
ist dies ein Gleichungssystem mit 4 Variablen, den Elementen in
, so
ist dies ein Gleichungssystem mit 4 Variablen, den Elementen in 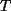 , und 4
Gleichungen. Man erhält als Lösung:
, und 4
Gleichungen. Man erhält als Lösung:
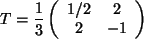 .
.
Eine neue Basis kann man als Matrix darstellen, indem man die Vektoren als
Spalten der Matrix schreibt:
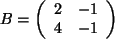 .
Dann ist
.
Dann ist
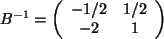 .
.
Eine lineare Abbildung 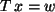 in der Originalbasis transformiert sich
nun zu
in der Originalbasis transformiert sich
nun zu
Setzt man in Symbolen:
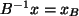 ,
,
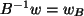 für die
Koordinaten in der neuen Basis, und
für die
Koordinaten in der neuen Basis, und
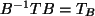 , dann ist
und es ist
, dann ist
und es ist
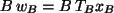 , also
, also
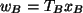 .
.
Dr.Wolfgang Quapp
2002-12-20
![]() in der Originalbasis transformiert sich
nun zu
in der Originalbasis transformiert sich
nun zu