(a) Es ist
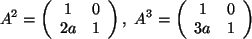 ,
und es besteht die Vermutung:
,
und es besteht die Vermutung:
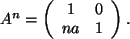 Der Beweis erfolgt über vollständige Induktion:
Der Beweis erfolgt über vollständige Induktion:
Ind.-Anfang: Die Vermutung ist richtig für 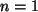 (und
(und 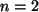 , und
, und 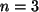 ).
).
Ind.-Voraussetzung: Die Vermutung ist richtig für  :
:
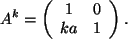
Ind.-Behauptung: Die Vermutung ist richtig für 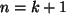 :
:
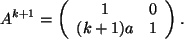
Ind.-Beweis:
Es ist
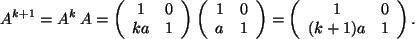 - Fertig -
- Fertig -
(b)
Es ist
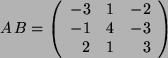 und
und
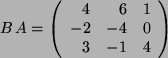 . Also gilt
. Also gilt
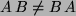 .
.
Dr.Wolfgang Quapp
2002-12-20
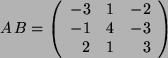 und
und
 . Also gilt
. Also gilt
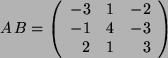 und
und
 . Also gilt
. Also gilt
![]() .
.