(a) Sei 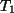 :
:
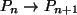 eine Abbildung vermittels
eine Abbildung vermittels
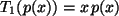 , wenn
, wenn
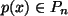 .
.
Behauptung: 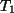 ist lineare Abbildung.
ist lineare Abbildung.
Seien
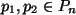 beliebige Polynome, dann ist
beliebige Polynome, dann ist
 , und mit
, und mit
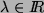 ist
ist
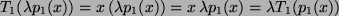 .
Also ist
.
Also ist 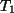 linear.
linear.
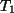 ist keine surjektive Abbildung, weil im Bild keine Konstanten
vorkommen.
ist keine surjektive Abbildung, weil im Bild keine Konstanten
vorkommen.
(b) Sei 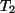 :
:
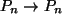 eine Abbildung vermittels
eine Abbildung vermittels
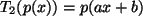 , wenn
, wenn
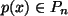 und
und
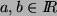 .
.
Behauptung: 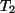 ist lineare Abbildung.
ist lineare Abbildung.
Seien
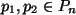 beliebige Polynome mit
beliebige Polynome mit
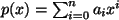 , und
, und
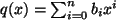 .
Dann ist
.
Dann ist
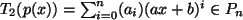 .
Für die Addition gilt:
Dann ist
.
Für die Addition gilt:
Dann ist
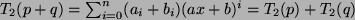 und für die Multiplikation mit einem Skalar:
und für die Multiplikation mit einem Skalar:
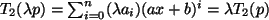 .
Also ist
.
Also ist 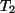 linear.
linear.
Dr.Wolfgang Quapp
2002-12-06