Verwende: Eine lineare Abbildung 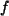 ist genau dann injektiv, wenn
ist genau dann injektiv, wenn
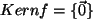 ist.
ist.
(i) Wären die Bildvektoren in 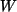 linear abhängig,
mit Zahlen
linear abhängig,
mit Zahlen
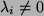 wäre dann also
Wegen der Linearität von
wäre dann also
Wegen der Linearität von 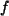 wäre dann
f(
wäre dann
f(
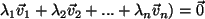 .
Da die
.
Da die 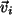 eine Basis von
eine Basis von 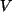 sind, ist das Argument in der Abbildung
nicht der Nullvektor, folglich hätte
sind, ist das Argument in der Abbildung
nicht der Nullvektor, folglich hätte 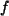 einen Kern ungleich 0, was ein
Widerspruch ist.
einen Kern ungleich 0, was ein
Widerspruch ist.
(ii) Sei 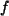 injektiv, d.h.
injektiv, d.h.
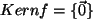 . Sei wieder (*) als Aufgabe
gestellt. Da nur
. Sei wieder (*) als Aufgabe
gestellt. Da nur
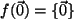 eindeutig gilt, und aus
eindeutig gilt, und aus
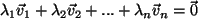 folgt, dass alle
folgt, dass alle
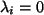 sind,
überträgt sich diese Gleichung auch auf (*), also sind die
sind,
überträgt sich diese Gleichung auch auf (*), also sind die
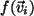 auch linear unabhängig.
auch linear unabhängig.
Dr.Wolfgang Quapp
2002-12-06