Die Vektoren
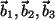 sind linear unabhängig:
sind linear unabhängig:
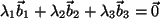 .
ergibt ein schlichtes System:
.
ergibt ein schlichtes System:
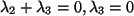 , und
zweimal
, und
zweimal
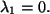
Damit können sie, genommen als lineare Hülle, einen Unterraum bilden, der dann
3-dimensional ist. Da die 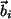 mit 4 Komponenten geschrieben sind, liegt
dieser Unterraum offenbar im
mit 4 Komponenten geschrieben sind, liegt
dieser Unterraum offenbar im 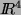 . Somit ist m=3, n=4.
. Somit ist m=3, n=4.
Dr.Wolfgang Quapp
2002-12-06