Seien
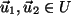 beliebige Vektoren.
beliebige Vektoren.
Nach Behauptung gilt für alle
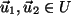 die
Eigenschaft:
die
Eigenschaft:
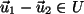 .
Es ist somit, wenn man zweimal
.
Es ist somit, wenn man zweimal 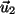 einsetzt:
einsetzt:
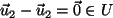 , und wenn man diesen Nullvektor
einsetzt, ergibt sich:
, und wenn man diesen Nullvektor
einsetzt, ergibt sich:
 .
Also gilt auch
.
Also gilt auch
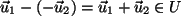 . Das ist die bisher
bekannte 2.Bedingung für die Untervektorraum-Eigenschaft. Diese ist somit
gezeigt.
. Das ist die bisher
bekannte 2.Bedingung für die Untervektorraum-Eigenschaft. Diese ist somit
gezeigt.
(Man braucht nicht vorauszusetzen, dass
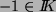 ist.)
ist.)
Dr.Wolfgang Quapp
2002-12-05