Es gelte 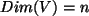 , und
, und
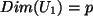 , mit
, mit 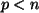 .
.
Dann gibt es 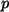 linear unabhängige Basisvektoren von U
linear unabhängige Basisvektoren von U .
Diese können auch als Teil
der Basis von
.
Diese können auch als Teil
der Basis von 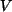 dienen. Dann fehlen aber noch
dienen. Dann fehlen aber noch  Basis-Vektoren in
Basis-Vektoren in 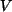 .
Diese können nach dem Basisergänzungssatz so gefunden werden,
dass sie nicht in U
.
Diese können nach dem Basisergänzungssatz so gefunden werden,
dass sie nicht in U sind:
sind:
Wähle Basis
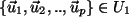 und
und
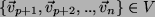 , aber
, aber
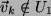 .
D.h., die
.
D.h., die 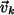 sind linear unabhängig von
den
sind linear unabhängig von
den 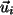 .
.
Setze
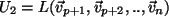 die lineare Hülle aller
die lineare Hülle aller 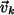 .
Aus der Konstruktion folgt, dass
.
Aus der Konstruktion folgt, dass 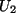 Untervektorraum von V ist, und seine
Dimension ist gleich der Anzahl der
Untervektorraum von V ist, und seine
Dimension ist gleich der Anzahl der 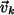 , nämlich
, nämlich  .
Da galt
.
Da galt
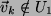 , ist der Durchschnitt
, ist der Durchschnitt
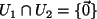 ,
und per Konstruktion ist die direkte Summe
,
und per Konstruktion ist die direkte Summe  =V, weil eben
=V, weil eben
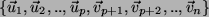 die Basis von V ist.
die Basis von V ist.
Dr.Wolfgang Quapp
2002-12-05