
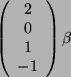
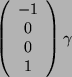
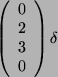
 |
+
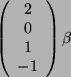 |
+
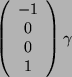 |
+
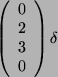 |
=
|
Dies ist ein homogenes Gleichungssystem:
| I: | + |
+ |
+ |
= 0 | |
| II: | + |
+ |
+ |
= 0 | |
| III: | + |
+ |
+ |
= 0 | |
| IV: | + |
+ |
+ |
= 0 |
aus II folgt:
![]() ,
,
in III folgt: -3
![]() , also
, also ![]() .
.
Damit folgt aus I:
![]() .
Und noch aus IV:
.
Und noch aus IV:
![]() , also auch
, also auch
![]() und
und
![]() .
Folglich sind die vier Vektoren linear unabhängig.
.
Folglich sind die vier Vektoren linear unabhängig.