- a)
- Ja, es gibt linear unabhängige Vektoren, da zwei Vektoren nur eine
Ebene aufspannen können.
Z.B.der Normalvektor zur Ebene durch die beiden
Vektoren
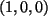 und
und 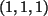 ist nicht linear kombinierbar.
Er ergibt sich aus dem Vektorprodukt:
ist nicht linear kombinierbar.
Er ergibt sich aus dem Vektorprodukt:
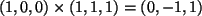 .
Aber auch schiefe Vektoren zur angegebenen Ebene sind linear unabhängig.
.
Aber auch schiefe Vektoren zur angegebenen Ebene sind linear unabhängig.
- b, c, e)
- Die drei Vektoren sind linear unabhängig. Sie spannen deshalb
den
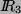 vollständig auf.
Alle weiteren Vektoren sind beschreibbar und
damit linear abhängig.
vollständig auf.
Alle weiteren Vektoren sind beschreibbar und
damit linear abhängig.
- d)
- Die vier Vektoren müssen schon untereinander linear abhängig sein.
Dabei sind aber die Vektoren 1, 2, und 4 im
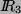 linear unabhängig.
Alle weiteren Vektoren sind damit linear abhängig.
linear unabhängig.
Alle weiteren Vektoren sind damit linear abhängig.
Dr.Wolfgang Quapp
2002-11-26