- a)
- Einfachster Schluss: Der Nullvektor muss in
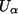 sein, also muss
sein, also muss 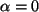 sein.
sein.
- b)
- Sei nun
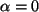 .
Betrachte 2 beliebige Vektoren der Ebene:
.
Betrachte 2 beliebige Vektoren der Ebene:
 mit:
mit: 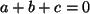 , und
, und
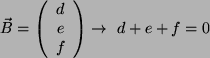 .
.
Ihre Summe ist
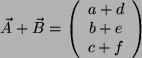 .
.
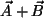 in die Ebene eingesetzt ist:
in die Ebene eingesetzt ist:
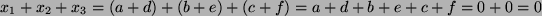 .
.
Analog gilt
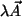 erfüllt
erfüllt
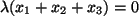 .
Wenn
.
Wenn 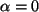 dann sind alle Unter-Vektorraum-Bedingungen erfüllt.
dann sind alle Unter-Vektorraum-Bedingungen erfüllt.
Dr.Wolfgang Quapp
2002-11-26
 mit:
mit: 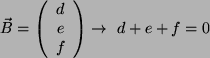 .
.
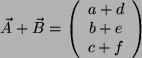 .
.
 mit:
mit: 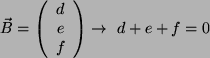 .
.
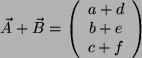 .
.