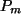 sei die Menge der Polynome mit reellen Koeffizienten vom
Grad
sei die Menge der Polynome mit reellen Koeffizienten vom
Grad 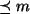 . Elemente
. Elemente 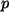 ,
, 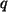 und
und  aus
aus 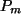 sind
sind
 ,
,
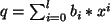 , und
, und
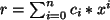 , mit
, mit
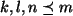 . Dabei sind
. Dabei sind 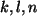 natürliche Zahlen, und
natürliche Zahlen, und
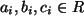 .
Auch
.
Auch  kann man sich in
kann man sich in 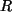 vorstellen.
vorstellen.
Die Addition + ist definiert durch:
+:
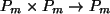 ,
,
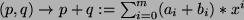 , und die Multiplikation * eines Polynoms
, und die Multiplikation * eines Polynoms 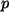 mit einer
reellen Zahl
mit einer
reellen Zahl 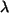 ist definiert durch:
ist definiert durch:
*:
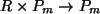 ,
,
 .
.
Zu zeigen ist, dass 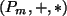 ein Vektorraum ist. Mit den genannten Definitionen ist klar, dass
ein Vektorraum ist. Mit den genannten Definitionen ist klar, dass 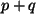 und
und
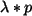 Elemente von
Elemente von 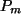 sind,
denn durch beide Operationen erhöht sich der Grad des Polynomes nicht.
Dadurch ist die Erfüllung der Axiome begründet:
sind,
denn durch beide Operationen erhöht sich der Grad des Polynomes nicht.
Dadurch ist die Erfüllung der Axiome begründet:
- (1)
-
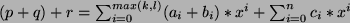
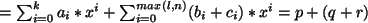 ,
,
gilt für alle
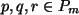 , da die Assoziativität für die reellen
Koeffizienten gilt. (Dabei ist etwa
, da die Assoziativität für die reellen
Koeffizienten gilt. (Dabei ist etwa 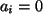 zu setzen, wenn
zu setzen, wenn 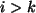 ist.)
ist.)
- (2)
-
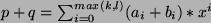
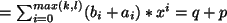 ,
,
gilt für alle
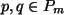 , da die Kommutativität für die reellen
Koeffizienten gilt.
, da die Kommutativität für die reellen
Koeffizienten gilt.
- (3)
- O ist der Nullvektor in
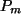 , bei dem alle
, bei dem alle 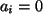 sind.
sind.
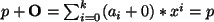 ,
gilt für alle
,
gilt für alle 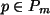 .
.
- (4)
- Zu jedem
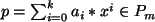 gibt es ein
gibt es ein
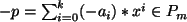 mit
mit
 .
.
- (5)
- Wenn
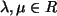 , dann ist
, dann ist
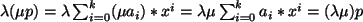 ,
gilt für alle
,
gilt für alle 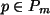 .
.
- (6)
- Die Eins
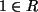 ergibt
ergibt
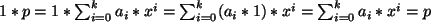 .
.
- (7)
- Wenn
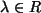 ist, gilt
ist, gilt
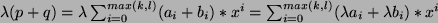
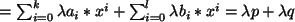 ,
für alle
,
für alle
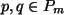 .
.
- (8)
- Wenn
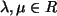 , dann ist
, dann ist
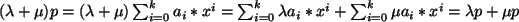 für alle
für alle 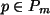 .
.
Damit ist gezeigt, dass 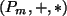 ein Vektorraum ist.
ein Vektorraum ist.
Dr.Wolfgang Quapp
2002-11-15