Der Unterraum ist durch
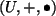 definiert, bestehend aus
definiert, bestehend aus 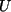 , einer Verknüpfung
, einer Verknüpfung 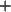 (Addition)
und einer Verküpfung
(Addition)
und einer Verküpfung  (Skalarmultiplitaktion).
(Skalarmultiplitaktion).
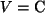 ;
;
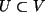 ;
;
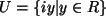 .
Die Definition für komplexe Zahlen
.
Die Definition für komplexe Zahlen
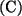 lautet
lautet 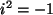 , sie wird
aber hier gar nicht zur Anwendung gebracht!
, sie wird
aber hier gar nicht zur Anwendung gebracht!
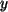 ist der Parameter, und zu
ist der Parameter, und zu
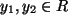 gilt
gilt
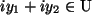 als auch
als auch
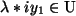 , wenn
, wenn
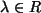 war.
D.h. dass
war.
D.h. dass
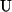 Untervektorraum ist,
Untervektorraum ist,
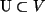 . Zusätzlich gelten auch alle 8 Axiome für Vektorräume.
. Zusätzlich gelten auch alle 8 Axiome für Vektorräume.
Bsp:
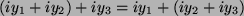 , u.s.w.
, u.s.w.
Durch die Erfüllung all dieser Bedingungen kann die Aussage bestätigt
werden:
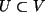 .
.
Dr.Wolfgang Quapp
2002-11-15