- a)
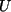 ist Untervektorraum.
ist Untervektorraum.
Begründung: Wähle Darstellung der Elemente von 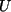 mit Parametern
mit Parametern 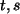 :
:
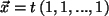 ,
,
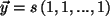 ,
, 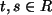 .
Dann ist
.
Dann ist
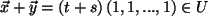 ,
und mit
,
und mit
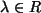 ist auch
ist auch
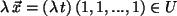 , u.s.w..
Alle Untervektorraumaxiome sind erfüllt.
, u.s.w..
Alle Untervektorraumaxiome sind erfüllt.
- b)
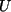 ist kein Untervektorraum.
ist kein Untervektorraum.
Begründung: Eine Linearkombination gewisser Elemente führt heraus.
Wähle Darstellung der Elemente von 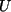 mit Parametern
mit Parametern 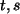 :
:
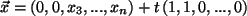 ,
,
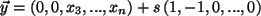 ,
,
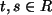 als auch
als auch
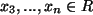 , beliebige Zahlen.
Für beliebige
, beliebige Zahlen.
Für beliebige 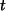 liegen alle
liegen alle 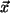 in
in 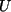 , und für beliebige
, und für beliebige  liegen alle
liegen alle 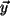 in
in 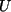 .
.
Aber
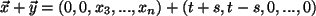 sind für
sind für
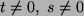 nicht in
nicht in 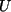 .
.
- c)
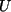 ist kein Untervektorraum, weil kein Nullvektor vorhanden ist.
ist kein Untervektorraum, weil kein Nullvektor vorhanden ist.
Dr.Wolfgang Quapp
2002-11-15