Sei
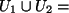 {
{
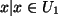 oder
oder 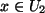 }
}
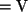 ,
,
und sei angenommen, dass 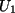 als auch
als auch  echte
Untervektorräume von
echte
Untervektorräume von
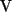 sind.
Dann gibt es ein Element
sind.
Dann gibt es ein Element 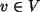 mit der Eigenschaft
mit der Eigenschaft
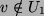 als auch
als auch
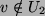 , folglich kann dieses
, folglich kann dieses  nicht in
nicht in
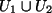 liegen. Das ist ein Widerspruch.
liegen. Das ist ein Widerspruch.
Die Aussage der 1.Zeile gilt nur, wenn 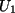 oder
oder  oder beide
oder beide
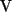 sind.
sind.
Dr.Wolfgang Quapp
2002-11-15