11.

Behauptung: 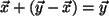$\vec{x}+(\vec{y}-\vec{x})=\vec{y}$ ( ! Druckfehler in Aufgabe !) Beweis durch Anwendung der Vektoraxiome:

(1)

Kommutativität: Es gilt
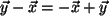$\vec{y}-\vec{x}=-\vec{x}+\vec{y}$, also ist $\vec{x}+(\vec{y}-\vec{x})= \vec{x}+(-\vec{x}+\vec{y})$

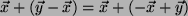
(2)

Assoizativität: $\vec{x}+(-\vec{x}+\vec{y})=(\vec{x}-\vec{x})+\vec{y}$

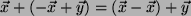
(3)

Existenz des inversen Elements, und eines Nullvektors: $\vec{x}+(-\vec{x})=\vec{O}$,
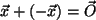für den dann gilt $\vec{O}+\vec{y}=\vec{y}$

(4)

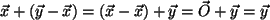
Also Fazit: 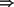$\vec{x}+(\vec{y}-\vec{x})= (\vec{x}-\vec{x})+\vec{y}=\vec{O}+\vec{y}=\vec{y}$ $\Rightarrow$ Die Behauptung ist richtig!