Die Aussage ist im allgemeinen falsch,
weil die in Frage kommende Relation nicht alle
Elemente erfassen braucht, aber die Reflexivität für alle Elemente
gelten muß.
Bsp.:
Sei
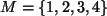 und
und
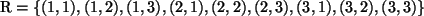 ,
,
dann ist
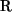 symmetrisch und transitiv, aber
symmetrisch und transitiv, aber
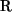 ist nicht reflexiv auf M weil 4
ist nicht reflexiv auf M weil 4
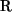 4 nicht gilt.
4 nicht gilt.
Dr.Wolfgang Quapp
2002-11-08