- (1)
- Wenn
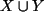 eine endliche Menge ist,
so müssen auch
eine endliche Menge ist,
so müssen auch 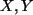 endliche Mengen sein:
endliche Mengen sein:
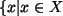 oder
oder 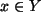 } .
} .
Wenn 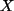 und/oder
und/oder 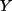 unendlich wären, so wäre
auch
unendlich wären, so wäre
auch 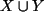 unendlich, weil bei der Vereinigung höchstens noch etwas
hinzu kommt.
unendlich, weil bei der Vereinigung höchstens noch etwas
hinzu kommt.
Oder betrachte Anzahl der Elemente:
 und
und
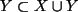 , also ist
, also ist
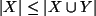 und
und
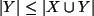 .
.
- (2)
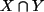 ist endlich, wenn
ist endlich, wenn 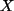 und
und 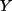 endlich sind.
endlich sind.
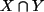 kann aber auch endlich sein,
wenn eine oder beide Mengen unendlich ist:
kann aber auch endlich sein,
wenn eine oder beide Mengen unendlich ist:
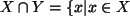 und
und 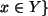 .
.
Bsp.:
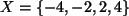 ,
,
 , und
, und
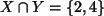 .
.
Für die Anzahl gilt nicht die Umkehrung obiger Relation, da
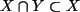 und
und
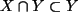 ist, können wenn
ist, können wenn 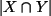 endlich ist, doch
endlich ist, doch  oder
oder 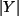 selbst unendlich sein.
selbst unendlich sein.
Dr.Wolfgang Quapp
2002-11-08