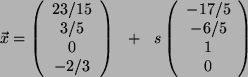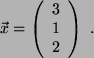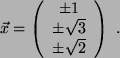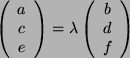Dr.Quapp
HS 2002
http://www.mathe.uni-leipzig.de/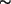 quapp/uebungenP.html
quapp/uebungenP.html
Lineare Algebra - Lösungen zur 11.Übung (zum 20.1.2003)
- 46.
- Eine Zeilenstufen-Berechnung führt bei Aufgabe (a) zu
also zum Rang 4 des homogenen Systems mit 4 Variablen,
folglich gibt es nur die triviale Null-Lösung.
- (b)
- Bei Aufgabe (b) ergibt sich
also ist das Gleichungssystem nicht eindeutig lösbar,
da 4 Variable vorliegen. Die Zeilenstufenform ergibt mit
dass
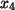 festgelegt ist zu
festgelegt ist zu
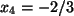 , dann aber
, dann aber 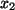 oder
oder 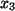 als Parameter
als Parameter  vorgegeben werden können.
Setze
vorgegeben werden können.
Setze 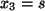 , dann folgt
, dann folgt
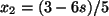 und
und
 .
Folglich ergibt sich als Lösungsvektor:
.
Folglich ergibt sich als Lösungsvektor:
- (c)
- Die Zeilenstufenform ergibt
Folglich ergibt sich als Lösungsvektor:
- 47.
- Setze vorerst
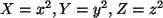 , und betrachte das System
als ein lineares System für die grossen Variablen.
Die Zeilenstufenform ergibt
Dann ist
, und betrachte das System
als ein lineares System für die grossen Variablen.
Die Zeilenstufenform ergibt
Dann ist 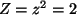 , also
, also
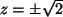 , sowie
, sowie
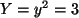 , also
, also
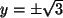 , und
, und
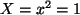 , also
, also 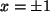 Folglich ergibt sich als Lösungsvektor:
Folglich ergibt sich als Lösungsvektor:
- (b)
- Die Matrix
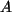 besteht aus 2 Spaltenvektoren, die im
besteht aus 2 Spaltenvektoren, die im 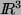 liegen.
Deren Linearkombination durch 2
liegen.
Deren Linearkombination durch 2  Werte
Werte
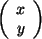 kann nur den Nullvektor ergeben, wenn die beiden Spaltenvektoren linear
abhängig sind, d.h.wenn sie auf einer Linie liegen, man sagt kollinear sind.
Im Fall a) sind die beiden Spaltenvektoren linear unabhängig, dann ist
kann nur den Nullvektor ergeben, wenn die beiden Spaltenvektoren linear
abhängig sind, d.h.wenn sie auf einer Linie liegen, man sagt kollinear sind.
Im Fall a) sind die beiden Spaltenvektoren linear unabhängig, dann ist
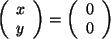 der Nullvektor die einzige mögliche Lösung.
der Nullvektor die einzige mögliche Lösung.
Im Fall b) sind die beiden Spaltenvektoren linear abhängig,
also alle Geraden fallen zu einer einzigen Geraden zusammen.
Es ist somit
Und wenn man
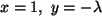 setzt, ergibt sich der Nullvektor.
setzt, ergibt sich der Nullvektor.
- 48.
- Gegeben sei eine quadratische Matrix
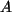 über
über
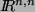 ,
und es werde das
Gleichungssystem
,
und es werde das
Gleichungssystem
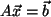 betrachtet.
betrachtet.
Beh.: 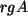 ist maximal
ist maximal
 Es existiert genau eine
eindeutige Lösung.
Es existiert genau eine
eindeutige Lösung.
Bew.:
(i) Hinrichtung: Sei 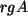 maximal. Da
maximal. Da
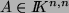 , folgt
, folgt
 , und da
, und da
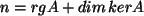 ist, muss somit
ist, muss somit
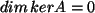 sein.
sein.
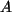 ist eineindeutige Abbildung, und genau ein
ist eineindeutige Abbildung, und genau ein 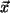 wird durch
wird durch 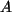 auf ein
auf ein 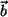 abgebildet.
abgebildet.
Es existiert genau eine eindeutige Lösung.
(ii) Rückrichtung: Es existiere genau eine eindeutige Lösung.
D.h.genau ein 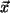 wird durch
wird durch 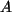 auf ein
auf ein 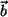 abgebildet. Dann ist
abgebildet. Dann ist 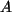 eine eineindeutige Abbildung,
für die gelten muss
eine eineindeutige Abbildung,
für die gelten muss
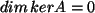 .
Da gilt
.
Da gilt
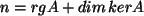 , ist somit
, ist somit  ,
und dieser Rang ist maximal.
,
und dieser Rang ist maximal.
q.e.d.
- 49.
- Der Vektor der rechten Seite ist nicht der Nullvektor, folglich ist das System
nicht lösbar, wenn
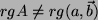 ist. Das tritt ein bei
ist. Das tritt ein bei
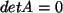 .
.
Fall (i)
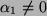 .
.
Es ergibt sich die Determinante:
Sie ist ungleich Null bei
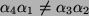 .
.
Fall (ii)
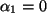 .
.
Dann ist die Determinante, wie man sofort sieht, dann nicht Null, wenn
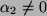 und
und
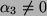 ist.
ist.
Lösung:
Wir haben 4 Gleichungen eines inhomogenen Systems für 4
Koeffizienten.
Sei (i) wieder
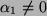 . Aus der letzen Stufe folgt
. Aus der letzen Stufe folgt
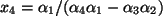 , dann
, dann
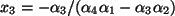 , sowie
, sowie
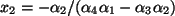 , und
, und
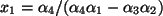 .
.
Im Fall (ii)
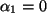 ergibt sich die analoge Formel mit diesem konkreten
Wert für
ergibt sich die analoge Formel mit diesem konkreten
Wert für 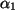 .
.
Dr.Wolfgang Quapp
2003-01-31
![]() quapp/uebungenP.html
quapp/uebungenP.html