Dr.Quapp: Statistik für Mathematiker mit SPSS
Hinweise zur Theorie der Stichproben
1.]
Es wird eine Stichprobe vom Umfang 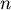 gezogen für eine
gezogen für eine
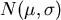 -verteilte Stichprobenvariable
-verteilte Stichprobenvariable 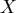 mit Erwartungswert
mit Erwartungswert
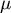 und Varianz
und Varianz 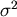 .
Geben Sie die Verteilung der folgenden Zufallsvariablen an:
.
Geben Sie die Verteilung der folgenden Zufallsvariablen an:
- a)
-
ist der erwartungstreue
Schätzer von 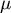 mit der Varianz
mit der Varianz
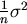 , d.h. die
Verteilung ist
, d.h. die
Verteilung ist
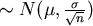 . Mit wachsendem
. Mit wachsendem 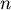 wird die Verteilung somit immer "schärfer".
wird die Verteilung somit immer "schärfer".
- b)
-
- c)
-
wegen der Aussagen in a).
- d)
-
ist die T- oder Students Verteilung, ohne "Verwendung" von 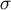 . Die
Verteilung ist angebracht, wenn
. Die
Verteilung ist angebracht, wenn 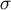 aus der Stichprobe als
aus der Stichprobe als 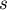 geschätzt werden muß.
geschätzt werden muß.
- e)
-
Die 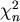 Verteilung entsteht durch
Setzen von
Verteilung entsteht durch
Setzen von
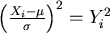 , wobei
, wobei
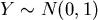 ist.
ist.
- f)
-
Die 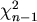 Verteilung ergibt sich, weil in der
Verteilung ergibt sich, weil in der
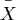 -Berechnung
noch ein Freiheitsgrad "verlorengeht". Der Ausdruck entspricht mit
-Berechnung
noch ein Freiheitsgrad "verlorengeht". Der Ausdruck entspricht mit
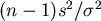 der Stichprobenverteilung der Varianz.
der Stichprobenverteilung der Varianz.
Dr.Wolfgang Quapp
2005-01-11
![]() gezogen für eine
gezogen für eine
![]() -verteilte Stichprobenvariable
-verteilte Stichprobenvariable ![]() mit Erwartungswert
mit Erwartungswert
![]() und Varianz
und Varianz ![]() .
Geben Sie die Verteilung der folgenden Zufallsvariablen an:
.
Geben Sie die Verteilung der folgenden Zufallsvariablen an: