Dr.Quapp: Statistik für Mathematiker mit SPSS

Hinweise zur Übung 16 No 1
Der zweidimensionale Zufallsvektor $(X,Y)$ besitze die Dichte

$$f(x,y)=\left\{ \begin{array}{rr} 1&x\ge 0,y\ge 0,8y+x\le 4\\ 0&\mbox{sonst} \end{array}\right..$$

a) Bestimmen Sie die beste Approximation von $Y$ durch $X$, d. h $E(Y\vert X)$ und den Fehler $E(Y-E(Y\vert X))^2$.
b) Bestimmen Sie die beste lineare Approximation $aX+b$ von $Y$ durch $X$ und den Fehler $E(Y-(aX+b))^2$.
c) Um wieviel Prozent vergr"o"sert sich der Fehler, wenn die die beste Approximation durch die beste lineare Approximation ersetzt wird.

Um die Aufgabe in SPSS auszutesten, verwenden wir Zufallszahlen, die das Gebiet der 2-dimensionalen Dichte $f(x,y)$ ausschöpfen. Am einfachsten gelingt das mit im Rechteck (4,1/2) gleichverteilten Zahlen, von denen die obere rechte Ecke abgeschnitten wird.

/* Eine Variable anzahl mit n=1023 Datens"atzen wird aktiviert  */
Input Program . 
LOOP #I=1 to 1023 . 
Compute anzahl=#I . 
FORMATS anzahl (F8).
END CASE . 
END LOOP . 
END FILE . 
END INPUT PROGRAM . 
EXECUTE . 

/* Erzeugung gleichm"assig verteilter Zufallszahlen "uber dem Dreieck */
COMPUTE x0 = RV.UniFORM(0,4) .
COMPUTE y0 = RV.UniFORM(0,0.5) .
IF( 8*y0+x0<=4) x=x0. 
IF( 8*y0+x0<=4) y=y0.
IF( 8*y0+x0<=4) anxy=1.
FORMATS anxy (F8).
EXECUTE.
USE ALL.
 FILTER BY anxy .
EXECUTE .

/* Zeichne das Dreieck mit der Dichte 1 */ 
GRAPH
  /SCATTERPLOT(bivar)= x with y
  /TITLE="Zufallspunkte (x,y) fuellen Dichte aus"
  /MISSING=LISTWISE .

Man kann die Zufallszahlen auch in einem Balkendiagramm darstellen, wenn man sie in 10 oder 11 Klassen diskretisiert:
$\rightarrow$

 COMPUTE xgrup = RND(2.5*x)/2.5 .
/* Theorie bedingte Erwartung von y bez.x: bthyx */
COMPUTE bthyx= (4-x)/16 .
EXECUTE .

Die theoretische Erwartung von $y$ bez.$x$ ist die Hälfte unter der Randverteilungsgeraden. Die Randverteilungen sind

$$f(x, \cdot )=\int f(x,y) dy = \int_0^{1/2-1/8 x} 1 dy = \frac{1}{2}-\frac{1}{8} x$$

und

$$f( \cdot ,y)= \int_0^{4-8 y} 1 dx = 4-8 y ,$$

also ist

$$E(Y\vert X) = \displaystyle\frac{\int y f(x,y) dy} { f(x,\... ...{1}{2} - \frac{1}{8} x) } = \frac{1}{4}-\frac{1}{16} x .$$

Da die beste Approximation für $E(Y\vert X)$ eine Gerade ist, ist das auch die beste lineare Approximation. Also wäre man hier schon fertig. Aber man kann auch zur Übung in SPSS die beste lineare Approximation mit der Regressionsrechnung ausrechnen.

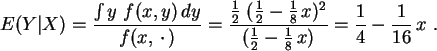
REGRESSION
  /MISSING LISTWISE
  /CRITERIA=PIN(.05) POUT(.10)
  /NOORIGIN
  /DEPENDENT y
  /METHOD=ENTER x
  /SAVE PRED .
RENAME VARIABLES (Pre_1=linAnpas).

Hier ist noch eingestellt, dass in $linAnpas$ die approximative Gerade abgelegt wird.
Nun können alle drei interessierenden Variablen in einem Balkendiagramm verglichen werden:

GRAPH
  /BAR(GROUPED)=MEAN(bthyx) MEAN(y) Mean(linAnpas) BY xgrup
  /MISSING=LISTWISE REPORT.

/* Bestimmung der Fehler */
COMPUTE fbErwth = (y- bthyx)**2 .
COMPUTE flinan  = (y- linanpas)**2 .
EXECUTE.
DESCRIPTIVES
  VARIABLES=fbErwth flinan 
  /STATISTICS=MEAN .

Als beste lineare Approximation ergibt sich eine Gerade sehr nahe an der theoretisch erwarteten Gerade $y= (4- x)/16$ . Auch die quadratischen Abweichungen sind nahe am erwarteten Wert von 1/96.