b) Erzeugen Sie mit dem Resultat aus a)
c) Erzeugen Sie mit dem in SPSS programmierten Zufallsgenerator
Hinweise zur 15. Übung No 2 + 3 - Exponentialverteilung -
2.]
a) Es sei ![]() . Zeigen Sie, daß
. Zeigen Sie, daß ![]() und
und ![]() exponentialverteilt sind mit dem Paramter
exponentialverteilt sind mit dem Paramter ![]() .
.
b) Erzeugen Sie mit dem Resultat aus a) ![]() Zufallszahlen in SPSS.
Zufallszahlen in SPSS.
c) Erzeugen Sie mit dem in SPSS programmierten Zufallsgenerator
![]() exponentialverteilte Zufallszahlen. Vergleichen Sie die
Resultate; insbesondere Modalwert und Median.
exponentialverteilte Zufallszahlen. Vergleichen Sie die
Resultate; insbesondere Modalwert und Median.
Zu a) Es sei ![]() , also ist
, also ist
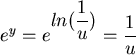 und
und
![]() .
Die Ableitung ist
.
Die Ableitung ist
![]() . Somit wird mit der Dichte 1 von
. Somit wird mit der Dichte 1 von ![]() über dem Intervall von (0,1)
über dem Intervall von (0,1)
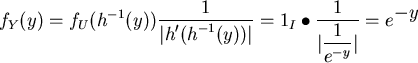
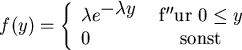
zu b+c) Mit u= RV.UNIFORM(0,1) und der Berechnung der zwei Versionen von Y1
und Y2 kann man davon ausgehen, daß man zufallsverteilte Zahlen erhalten
hat, die einer Exponantialverteilung folgen. Dies beruht auf der
Inversionsmethode. Verschafft man sich noch mit ee=RV.EXP(1) entsprechende
zufallsverteilte Zahlen von SPSS, so kann man alle drei vergleichen:
In einem Test ergab sich als Resultat:
Für Y1 der Mittelwert=0.961, Median=0.748, und Modalwert=0.004 .
Für Y2 der Mittelwert=1.151, Median=0.641, und Modalwert=0.009 .
Für EE der Mittelwert=0.950, Median=0.611, und Modalwert=0.010 .
Das ist natürlich nur ein Vergleich der Zufallszahlen, noch dazu mit einer
"geringen" Anzahl, aber die Übereinstimmung ist schon gut.
Mittels Darstellung durch Histogramme kann man sich auch graphisch davon
überzeugen.
Wenn die Exponentialverteilung zur Beschreibung des radioaktiven Zerfalls
verwendet wird, entspricht der Median der Halbwertszeit, der Zeit, in der
die Hälfte einer Menge eines radioaktiven Elementes umgewandelt worden
ist. Es ist mit der Verteilungsfunktion
3.]
Es seien
![]() ,
, ![]()
a) Zeigen Sie, daß ![]() eine erwartungstreue
Schätzung für
eine erwartungstreue
Schätzung für ![]() ist.
ist.
b) Zur Schätzung von ![]() wählt man die relative Häufigkeit
der entsprechenden Ereignisse. Welche Eigenschaften hat diese Schätzung?
wählt man die relative Häufigkeit
der entsprechenden Ereignisse. Welche Eigenschaften hat diese Schätzung?
c) Zur Schätzung von ![]() gibt es weiterhin den Ansatz
gibt es weiterhin den Ansatz
zu a)
Sind n Zufallszahlen ![]() wie oben gegeben, so ist der Mittelwert
wie oben gegeben, so ist der Mittelwert
![]() und sein Erwartungswert ist nach dem schwachen Gesetz der großen Zahlen
und sein Erwartungswert ist nach dem schwachen Gesetz der großen Zahlen
zu b)
Die Exponantialverteilung beschreibt Ausfallprozesse, d.h.man wird
besonders an der "vorderen" Kante der Verteilung interessiert sein: Wie
viele Geräte fallen nach dem ersten Einschalten etwa für ![]() aus?
aus?
Sei also
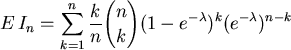
zu c)
Sei
![]() .
.
Dessen Erwartungswert ist mit unseren Mitteln unberechenbar. Also bleibt nur
der "experimentelle" Test mit SPSS.