Hinweise zur 12. Übung - Regression mit
Konfidenzintervallen und
![]() -Anpassung -
-Anpassung -
1.] Der "Schiefe Turm" von Pisa wurde im Dezember 2001 nach langer
Behandlung wieder für Besucher freigegeben. Folgende Meßreihe
schildert das dramatische Vorgeschehen. Angegeben ist die Schiefe ![]() in
Addition zu 2,90
in
Addition zu 2,90![]() in
in ![]() .
. ![]() sind die Jahreszahlen. 1975 betrug die
Schiefe also 2,9642
sind die Jahreszahlen. 1975 betrug die
Schiefe also 2,9642 ![]() .
.
| x | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 |
| y | 6,42 | 6,44 | 6,56 | 6,67 | 6,73 | 6,88 | 6,96 | 6,98 | 7,13 | 7,17 | 7,25 | 7,42 | 7,57 |
.

.
(b) Geben Sie ein 95% Konfidenzintervall CI für den wahren
Anstieg ![]() an! Interpretieren Sie dieses Intervall.
an! Interpretieren Sie dieses Intervall.
Dieses CI wird im direkten ![]() Linearen Fit
Linearen Fit
![]() Button Statistik mitgeliefert, es
muß dort extra angeklickt werden. Das Intervall ist
Button Statistik mitgeliefert, es
muß dort extra angeklickt werden. Das Intervall ist
![]() (0.086,0.1).
Im ungünstigen Fall könnte die Schiefe also mit dem Anstieg 0.1 wachsen.
Bei dieser Methode kann das Konfidenzintervall für die
(0.086,0.1).
Im ungünstigen Fall könnte die Schiefe also mit dem Anstieg 0.1 wachsen.
Bei dieser Methode kann das Konfidenzintervall für die ![]() -Werte noch
variabel eingestellt werden, und außerdem kann unterschieden werden
zwischen individuellem CI per Regressor, und mittlerem CI.
-Werte noch
variabel eingestellt werden, und außerdem kann unterschieden werden
zwischen individuellem CI per Regressor, und mittlerem CI.
(c) Die mit dem Problem des "Schiefen Turms" befaßten Bauleute
waren 1987 naturgemäß an einer Aussage interessiert, um wie viele
![]() sich der Turm bis z.B. 1997 weiter neigen würde, wenn keinerlei
Korrekturen am Bau vorgenommen werden würden. Nutzen Sie die
Regressionsgerade für eine derartige Vorhersage.
sich der Turm bis z.B. 1997 weiter neigen würde, wenn keinerlei
Korrekturen am Bau vorgenommen werden würden. Nutzen Sie die
Regressionsgerade für eine derartige Vorhersage.
Es ist
![]() , und z.B.
y(104)= 9.08076cm, also im
Jahr 2004 wäre dieser Wert erwartet worden. (Aber 1990 hat man
mit ernsten Korrekturen begonnen, die ein langsames Zurückkippen von etwa
40
, und z.B.
y(104)= 9.08076cm, also im
Jahr 2004 wäre dieser Wert erwartet worden. (Aber 1990 hat man
mit ernsten Korrekturen begonnen, die ein langsames Zurückkippen von etwa
40![]() bewirkt haben.)
bewirkt haben.)
(d) Bestimmen Sie die Fehlergrenze für die vorhersagbare mittlere
Entwicklung der Schiefe im Jahr 1997 für ein 95% CI und ein 99% CI.
In ![]() Methode Kurvenanpassung (Linear)
Methode Kurvenanpassung (Linear)
![]() Speichern
Speichern ![]() Vorhergesagte Werte,
Vorhersageintervalle ist eine Lösung dieser Teilaufgabe "automatisch"
möglich. Man hat als
Vorhergesagte Werte,
Vorhersageintervalle ist eine Lösung dieser Teilaufgabe "automatisch"
möglich. Man hat als ![]() -Achse zuerst die Variable
-Achse zuerst die Variable ![]() einzusetzen, dann
aber die weitere Möglichkeit
einzusetzen, dann
aber die weitere Möglichkeit ![]() Zeit anzuklicken.
SPSS verwendet dann die bisherigen Zeilen der Datentabelle als
Zeitschritte, also hier 13. Damit kann im
Fenster
Zeit anzuklicken.
SPSS verwendet dann die bisherigen Zeilen der Datentabelle als
Zeitschritte, also hier 13. Damit kann im
Fenster ![]() Speichern die Anzahl der weiteren Zeitschritte für
eine Vorhersage angegeben werden. Wir haben Daten für 13 Jahre bis 1987,
also sind bis 1997 dann 23 Zeitschritte einzugeben. Auch
Konfidenzintervalle können in diesem Fenster angeklickt werden, und
das CI-Niveau ist stufenweise einstellbar.
Speichern die Anzahl der weiteren Zeitschritte für
eine Vorhersage angegeben werden. Wir haben Daten für 13 Jahre bis 1987,
also sind bis 1997 dann 23 Zeitschritte einzugeben. Auch
Konfidenzintervalle können in diesem Fenster angeklickt werden, und
das CI-Niveau ist stufenweise einstellbar.
2.]
(a) Erzeugen Sie die ![]() -Verteilung mit 4
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen
-Verteilung mit 4
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen ![]() Verteilung
über einer Achse zum Intervall (0,15).
Verteilung
über einer Achse zum Intervall (0,15).
(b) Bei der Untersuchung über den Schädlingsbefall von Apfelbäumen wurden
drei verschiedene Apfelesorten (A,B,C) überprüft.
Es wurden insgesamt ![]() Bäume untersucht. Es ergab sich folgende Kontingenztafel:
Bäume untersucht. Es ergab sich folgende Kontingenztafel:
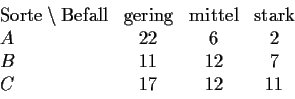
Das Problem besteht darin zu vergleichen, ob gleichzeitig die neun
Werte B![]() bis B
bis B![]() des Befalls einer entsprechenden
Unabhängigkeits-Bedingung, hier für eine Zähldichte p
des Befalls einer entsprechenden
Unabhängigkeits-Bedingung, hier für eine Zähldichte p![]() ,
, ![]() ,
genügen.
Die p
,
genügen.
Die p![]() ergeben sich bei einer Kreuztabelle als Produkte der
jeweiligen Randverteilungen.
Wie bei anderen Tests sucht man nach einer eindimensionalen
Testgröße, mit der man die Gesamtschwankung adäquat wiedergeben
kann. Betrachtet man etwa
ergeben sich bei einer Kreuztabelle als Produkte der
jeweiligen Randverteilungen.
Wie bei anderen Tests sucht man nach einer eindimensionalen
Testgröße, mit der man die Gesamtschwankung adäquat wiedergeben
kann. Betrachtet man etwa
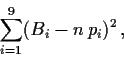
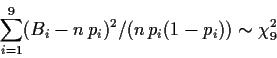
zu (a) Die 151.Zeile ist anzuklicken, und die Achsenvariable
![]() =($casenum-1)/10 zu setzen. Mit chi4=CDF.CHISQ(x,4)
haben wir die Verteilungsfunktion, und mit chi4di=Diff(chi4)
in
=($casenum-1)/10 zu setzen. Mit chi4=CDF.CHISQ(x,4)
haben wir die Verteilungsfunktion, und mit chi4di=Diff(chi4)
in ![]() Berechnen, Zeitreihen ergibt sich die Dichte.
In der kumulativen Verteilungsfunktion kann man sofort den Wert ablesen, der
bei dem gängigen 95% CI gilt: Es ist 9.48.
Analoges kann
man für No.3 unten mit 5 Freiheitsgraden (df) rechnen.
Berechnen, Zeitreihen ergibt sich die Dichte.
In der kumulativen Verteilungsfunktion kann man sofort den Wert ablesen, der
bei dem gängigen 95% CI gilt: Es ist 9.48.
Analoges kann
man für No.3 unten mit 5 Freiheitsgraden (df) rechnen.
zu (b) Zuerst muß das Problem gelöst werden, wie man SPSS die
Kreuztabelle beibringt! Dazu sind alle ![]() Fälle einzeln als Zeilen
einzugegeb. (Hinweis: Datei in D: spss122.sav leistet dies. - Wenn
man mit gewichteten Fällen arbeitet, ginge es etwas schneller:
Datei in D: apfel9.sav).
Fälle einzeln als Zeilen
einzugegeb. (Hinweis: Datei in D: spss122.sav leistet dies. - Wenn
man mit gewichteten Fällen arbeitet, ginge es etwas schneller:
Datei in D: apfel9.sav).
Bei ![]() Deskriptive Statistik, Kreuztabelle kann dann die in der
Aufgabe gegebene Tabelle erzeugt werden.
Im Fenster
Deskriptive Statistik, Kreuztabelle kann dann die in der
Aufgabe gegebene Tabelle erzeugt werden.
Im Fenster ![]() Statistik muß der Chi-Square Test angeklickt
werden.
Es resultieren je nach Methode zwei Werte: 10.7 oder 11.3, beide sind
größer als der kritische Wert 9.48, also kann die
Nullhypothese einer
Unabhängigkeit des Befalls von der Sorte nicht bestätigt werden.
Die Zahl der Freiheitsgrade DF ist dabei (m-1)(n-1) mit m Zeilen und n
Spalten in der Kreuztabelle. Der Test gibt die genaue "Signifikanz"
aus, die mit 2.96%, oder 2.33% auch "hinter" den 5% des
geforderten CI's liegt.
Statistik muß der Chi-Square Test angeklickt
werden.
Es resultieren je nach Methode zwei Werte: 10.7 oder 11.3, beide sind
größer als der kritische Wert 9.48, also kann die
Nullhypothese einer
Unabhängigkeit des Befalls von der Sorte nicht bestätigt werden.
Die Zahl der Freiheitsgrade DF ist dabei (m-1)(n-1) mit m Zeilen und n
Spalten in der Kreuztabelle. Der Test gibt die genaue "Signifikanz"
aus, die mit 2.96%, oder 2.33% auch "hinter" den 5% des
geforderten CI's liegt.
Im Falle der Unabhängigkeit von Schädlingsbefall und Sorte hätte
man die folgende Tabelle vorgefunden (mit den gleichen Randverteilungen
/100 wie oben)
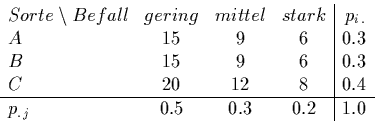
Abschließende Frage: "Wo kaufen Sie Ihre Äpfel?"
Antwort: "Wer keine weiche Birne hat, kauft harte Äpfel aus
Halberstadt."
3. ]
(a)
Erzeugen Sie die ![]() -Verteilung mit 5
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen
-Verteilung mit 5
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen ![]() Verteilung
über dem Intervall
Verteilung
über dem Intervall ![]() (0,15).
(0,15).
(b) Erzeugen Sie für das Merkmal X ![]() Würfel
je 600 Zufallszahlen.
(Anleitung: Gleichverteilung im Intervall (1.0,6.999) auf ganze Zahlen
reduzieren.)
Würfel
je 600 Zufallszahlen.
(Anleitung: Gleichverteilung im Intervall (1.0,6.999) auf ganze Zahlen
reduzieren.)
Zeichnen Sie ein Histogramm für die sechs Kategorien von X, und
überprüfen Sie die Gleichheit der Ausprägungen der
einzelnen Augenzahlen mit dem ![]() -Anpassungstest.
-Anpassungstest.
Zur Theorie: Siehe No.2.
Zu (a) siehe ebenfalls No.2.
Zu (b) Mit W=TRUNC(RV.UNIFORM(1,6.9999)) erhalten wir den zufälligen
Würfel. In den Tests sollte dann eben der
![]() Chi-Quadrat-Test angeklickt werden (in
Chi-Quadrat-Test angeklickt werden (in
![]() Nichtparametrische Tests),
und in diesem ist nur noch darauf zu achten, daß beim voreingestellten
Button angeklickt ist, daß alle Kategorien gleich sein sollen
(Nullhypothese): D.h.hier soll gelten
Nichtparametrische Tests),
und in diesem ist nur noch darauf zu achten, daß beim voreingestellten
Button angeklickt ist, daß alle Kategorien gleich sein sollen
(Nullhypothese): D.h.hier soll gelten ![]() für i=1,...,6.
Es resultieren bei mehreren Tests Chi-Quadrat-Werte von 1.84 bis 8.21,
alle Werte sind kleiner gewesen als der kritische
Wert von 11.07 für 95% CI bei 5 Freiheitsgraden.
Die ausgegebene Signifikanz ist mit 0.87 (entsprechend 87%
für i=1,...,6.
Es resultieren bei mehreren Tests Chi-Quadrat-Werte von 1.84 bis 8.21,
alle Werte sind kleiner gewesen als der kritische
Wert von 11.07 für 95% CI bei 5 Freiheitsgraden.
Die ausgegebene Signifikanz ist mit 0.87 (entsprechend 87% ![]() 5% CI)
bis 0.18 sehr hoch bis hoch.
Also kann die Nullhypothese nicht verworfen werden, das unser SPSS-Würfel
"ehrlich" arbeitet.
5% CI)
bis 0.18 sehr hoch bis hoch.
Also kann die Nullhypothese nicht verworfen werden, das unser SPSS-Würfel
"ehrlich" arbeitet.