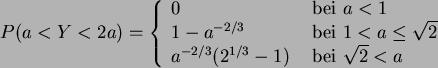a) Bestimmen Sie die Einzelwahrscheinlichkeiten
b) Erzeugen Sie dieses Experiment mit SPSS, indem Sie drei Variable
c) Mit
Hilfe zur 7. Übung - Operationen mit Zufallsvariablen
1.]
Es sei ![]() die summierte Augenzahl beim Wurf mit 3 Würfeln.
die summierte Augenzahl beim Wurf mit 3 Würfeln.
a) Bestimmen Sie die Einzelwahrscheinlichkeiten ![]() für
für ![]() .
Für welches
.
Für welches ![]() ist
ist ![]() maximal?
maximal?
b) Erzeugen Sie dieses Experiment mit SPSS, indem Sie drei Variable ![]() und
und ![]() aus gleichmäßig verteilten Zufallszahlen erzeugen, und
aus gleichmäßig verteilten Zufallszahlen erzeugen, und ![]() als
Summe dieser Zufallszahlen darstellen.
Prüfen Sie das Resultat durch ein Balkendiagramm.
als
Summe dieser Zufallszahlen darstellen.
Prüfen Sie das Resultat durch ein Balkendiagramm.
c) Mit ![]() bezeichnen wir das Ereignis, daß bei einem Wurf
alle Augenzahlen unterschiedlich sind. Bestimmen Sie
bezeichnen wir das Ereignis, daß bei einem Wurf
alle Augenzahlen unterschiedlich sind. Bestimmen Sie ![]() und
bestimmen Sie
und
bestimmen Sie ![]() für
für ![]() .
.
Da die Zufallsvariablen addiert werden, muß ihre Verteilungsdichte aus
einer Faltung berechnet werden. Für zwei Zufallsvariable ![]() und
und ![]() ergibt sich beim Würfel:
ergibt sich beim Würfel:
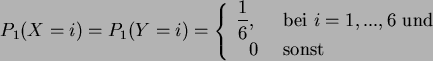
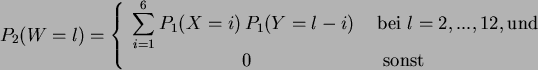
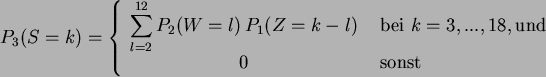
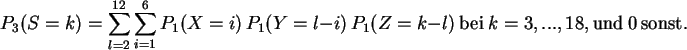
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||
|
|
1 | 3 | 6 | 10 | 15 | 21 | 25 | 27 | 27 | 25 | 21 | 15 | 10 | 6 | 3 | 1 |
zu b) Die Zufallsvariablen ![]() sind aus einer Gleichverteilung in
[1.0,6.9999] durch Abschneiden auf ganze Zahlen erzeugbar:
TRUNC(RV.UNIFORM(1,6.9999)). Man verwende etwa
216 Werte, oder Vielfache davon:
sind aus einer Gleichverteilung in
[1.0,6.9999] durch Abschneiden auf ganze Zahlen erzeugbar:
TRUNC(RV.UNIFORM(1,6.9999)). Man verwende etwa
216 Werte, oder Vielfache davon: ![]() .
.
zu c) Die Anzahl der günstigen Fälle ist eine Variation ohne Wiederholung
mit ![]() =6,
=6, ![]() =3, also 120 Fälle, damit ist
=3, also 120 Fälle, damit ist
![]() .
Die bedingte Wahrscheinlichkeit, wenn
.
Die bedingte Wahrscheinlichkeit, wenn ![]() eingetreten ist, kann leicht
abgezählt werden:
Bei
eingetreten ist, kann leicht
abgezählt werden:
Bei
![]() ist sie Null (diese Fälle kommen nicht vor),
bei
ist sie Null (diese Fälle kommen nicht vor),
bei ![]() ist sie je 3!,
bei
ist sie je 3!,
bei ![]() ist sie je
ist sie je ![]() , und
bei
, und
bei ![]() ist sie je
ist sie je ![]() .
.
In SPSS kann eine neue Variable definiert werden unter Zuhilfenahme des
Falls-Fensters: ![]()
![]() Falls
Falls
![]() ist.
Die Statistik von SB sollte obige Werte annähern. In einem Balkendiagramm kann
man
ist.
Die Statistik von SB sollte obige Werte annähern. In einem Balkendiagramm kann
man ![]() oder
oder ![]() ansehen, wobei bei letzterem noch unter
ansehen, wobei bei letzterem noch unter ![]() Optionen die
Darstellung der "Fehlenden Werte" abgeschaltet werden sollte.
Optionen die
Darstellung der "Fehlenden Werte" abgeschaltet werden sollte.
2.]
a) Für welche Werte ![]() ist
ist
![]() eine Dichte?
Bestimmen Sie die Verteilungsfunktion
eine Dichte?
Bestimmen Sie die Verteilungsfunktion ![]() zu dieser Dichte!
zu dieser Dichte!
b) Es sei ![]() . Bestimmen Sie die Dichte und
Verteilungsfunktion von
. Bestimmen Sie die Dichte und
Verteilungsfunktion von ![]() , wobei
, wobei ![]() die
Verteilungsfunktion aus a) ist (Inversionsmethode).
die
Verteilungsfunktion aus a) ist (Inversionsmethode).
c) Bestimmen Sie mir SPSS Modalwert, Median, und Quartile von ![]() .
Benutzen Sie dazu N=200 Werte von
.
Benutzen Sie dazu N=200 Werte von ![]() .
.
Es ist ![]() .
.
3.]
Berechnen Sie 200 Werte der Zufallsvariablen ![]() mit Gleichverteilung
mit Gleichverteilung
![]() mit etwa a=10.
Berechnen Sie die neue Zufallsvariable
mit etwa a=10.
Berechnen Sie die neue Zufallsvariable
Sei ![]() eine Zufallsvariable und
eine Zufallsvariable und ![]() , wobei
, wobei ![]() z.B. stückweise
monoton und differenzierbar sei. Dann ist die Dichte von
z.B. stückweise
monoton und differenzierbar sei. Dann ist die Dichte von ![]()