Dr.Quapp: Statistik für Mathematiker mit SPSS

Hinweise zur 4. Übung - Nichtlineare Regression und Partielle Korrelation

1.] a) Es seien $X_i$$\sim$ N(0,1) und $Y_i$$\sim$ N(0,1) unabhängige Zufallsgrößen. Wir bilden

$$W = a X + b Y \ \ {\rm und } \ \ V= a^\prime \ X + b^\prime \ Y .$$

Zeigen Sie, daß Cov(V,W)= a a$^\prime$ + b b$^\prime$ ist.
b) Erzeugen Sie 1000 Zufallszahlen von V und W. Wählen Sie dabei a, a$^\prime$, b, b$^\prime$ so, daß gilt

$$(i) \ \ \rho_{V,W} =0,2 {\rm\ \ bzw. \ \ } (ii) \ \rho_{V,W} =0,0 .$$

a) Die Kovarianz zweier Zufallsvariabler ist

$$Cov(W,V) = E( W\,V ) - EW \ EV = E \left( ( W - EW )( V - EV ) \right) .$$

Damit wird

$$Cov(W,V) = E \left( W V - W EV - V EW + EW EV \right) .$$

Es ist EX=0, EY=0, E(X Y)=0, (da X und Y unabhängig), VarX=1, und VarY=1, also EW=EV=0 und

$$Cov(W,V) = E \left( (a X + b Y) (a^\prime \ X + b^\prime \ Y ) \right) =$$

$$E \left( a a^\prime X^2 + b a^\prime X Y + a b^\prime Y X + b b^\prime Y^2 \right)=$$

$$a a^\prime E(X^2) + ( a b^\prime + b a^\prime) E(X Y) + b b^\prime E( Y^2) = a a^\prime + b b^\prime .$$

b) Der Fall (ii) ist theoretisch lösbar, wenn die beiden "Vektoren" W und V senkrecht aufeinander stehen: Die Parameter $a,\ a^\prime ,\ b, \ b^\prime$ sind entsprechend wählbar, etwa $a =\ a^\prime =0.5\sqrt{2}$ und $b =\ b^\prime = \pm 0.5\sqrt{2}$. (Da die Zufallsvariablen $X$ und $Y$ durch einen "praktischen" Zufallszahlengenerator bestimmt werden, sind sie nicht völlig unabhängig, also wird sich in der Lösung nicht exakt die Kovarianz 0 einstellen.)
Der Fall (i) ist aus der Gleichung für die Kovarianz bestimmbar. Der Korrelationskoeffizient $\rho$ ist

$$\rho_{W,V} = \frac{ Cov(W,V) }{ \sigma_W \ \sigma_V } = \fr... ...e } {\sqrt{ ( a^2 + b^2 ) ( a^{\prime\,2}+ b^{\prime\,2}) }}$$

Wird $\rho$=0.2 gesetzt, so können 3 Werte $(a, b, a^\prime)$ gesetzt werden, und der vierte wird berechnet. Z.B. $a =\ a^\prime =0.5\sqrt{2}$, b=1, ergibt $b^\prime = -0.3108$ .

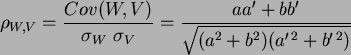
2.] Laden Sie die Datei HCN1.sav von D:. Die Werte sind experimentelle Resultate eines Spektrometers, mit welchem Vibrations-Rotationslinien des HCN-Moleküles gemessen wurden. Es wird aus theoretischen Betrachtungen geschlossen, daß einzelne Linien additiv überlagern, und die Bandenform mit der sogenannten Lorenz-Funktion beschrieben werden kann:

$${\rm basislinie} \ - \ \sum_i c_i \frac{a_i}{\displaystyle{(\frac{a_i}{2})^2 + (nr-b_i)^2 } }$$

Der Laufindex $i$ gibt die Nummerierung der entsprechenden Linie an, und $a_i, b_i, c_i$ sind für jede Linie zu findende Parameter: $b_i$ sind die Lageparameter, $c_i$ geben die Größe = Intensität der Linien an, und $a_i$ beschreiben die sogenannte Halbwertsbreite. $nr$ sei die Achsenvariable.

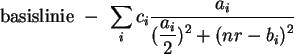
Inspektion der Daten im Streudiagramm oder Liniendiagramm zeigt, daß 3 Spektral-Linien vorhanden sind. Um diese mit der angegebenen Funktion anzupassen, müssen die zu verwendenden Start-Parameter geraten werden. Als erstes die Basislinie: sie sollte etwa be 0,975 sein. Die $b_i$ sind die Lageparameter, sie geben die Linienmittelpunkte an: diese werden bei 56, 124 und 184 sein (aufsteigend mit $nr$). Die $a_i$ sind die Halbwertsbreiten. Auch hier kann man direkt im Bild zu einer Näherung kommen, zu 10, 20, und 15. Verbleiben die Intensitätskoeffizienten c1, c2, und c3. Offensichtlich ist etwa die Relation zwischen ihnen, die 8 zu 3 zu 1 sein sollte. Die wahren Größen ergeben sich (aus mehreren Tests über Versuch und Irrtum) zu 0.33, 3.4, und 1.0.
Zum Fit selbst klickt man an:
, und kann im mittleren Fenster dann die Formel eintippen wie in der Aufgabe angegeben, wobei die Parameter in einem extra Fenster zu definieren und gleichzeitig numerisch zu belegen sind. (Achtung: Eigenartiges Verhalten des Systems zur Dezimaldarstellung: im Funktionenfenster gilt der american decimal point, aber im Parameterfenster das deutsche Dezimalkomma!!) Die Meßwerte-Variable, die die gesuchte Funktion ergeben soll, ist ins obere Kästchen als "Abh.Variable" zu schieben. Hier ist es die "Intensity", die Variable $intensit$. Folgendes Programm leistet auch diese Aufgabe (Hcn1.sps von D: ):

 NonLinear Regression. 
\* Startwerte der Parameter *\
 MODEL PROGRAM BALI=0.975  
               A1=10  A2=20  A3=15 
               B1=56  B2=124 B3=184
               C1=0.1 C2=1.0 C3=0.3 .
\* Fit-Funktion mit 10 Parametern *\ 
 COMPUTE PRED_ = bali-c1*a1/(a1**2/4+(nr-b1)**2)- 
                      c2*a2/(a2**2/4+(nr-b2)**2)- 
                      c3*a3/(a3**2/4+(nr-b3)**2). 
 NLR intensit  
   /PRED PRED_ 
   /SAVE PRED
   /CRITERIA SSCONVERGENCE 1E-8 PCON 1E-8 .
EXECUTE .

Der nichtlineare Fit liefert die Iterationsschritte, und wenn alles nahe genug an der Lösung eingegeben ist, liefert der Fit auch ein konvergentes Resultat. Es zeigt sich, daß die Intensitäten $c_i$ etwas zu gering geschätzt waren, aber der Fit konvergiert trotztdem!
(Aus dem Verlauf der Iteration kann eventuell auf falsche Startwerte der Parameter geschlossen werden. Wenn keine Konvergenz eintritt, hilft nur, das Modell immer weiter abzurüsten, bis der Fehler gefunden ist.)

Das Resultat kann verwendet werden, um die angepaßte Funktion grafisch mit den Daten zu vergleichen: Dazu mußte noch vor dem Fit im Fenster angeklickt werden, daß die Schätzung zu speichern ist. Die mit den gefitteten Parametern berechneten Funktionswerte stehen als pred$_1$ (oder mit weiteren Indizees bei mehreren Versuchen für die Rechnungen) in der Variablenliste und können vergleichend gezeichnet werden:

 GRAPH
  /LINE(MULTIPLE)= VALUE( intensit pred_1 ) BY nr .
EXECUITE .

Das Resultat für die Parameter steht unter "Estimate" wie folgt:

                                          Asymptotic 95 %
                          Asymptotic     Confidence Interval
  Parameter   Estimate    Std. Error     Lower         Upper

  BALI        ,984308167   ,000925529   ,982485194   ,986131140
  A1        15,003139309   ,831807690 13,364765819 16,641512799
  A2        23,034038216   ,155127065 22,728491544 23,339584888
  A3        17,170171547   ,322216877 16,535515731 17,804827364
  B1        55,838403476   ,255047262 55,336048572 56,340758380
  B2        124,03042063   ,046765860 123,93830806 124,12253320
  B3        184,22083959   ,097742433 184,02832080 184,41335839
  C1          ,326143201   ,014941219   ,296714167   ,355572236
  C2         3,400817086   ,019423380  3,362559745  3,439074426
  C3         1,045279896   ,016352100  1,013071914  1,077487878