welches die deskriptive Statistik ermöglicht. Schiebe puls in rechtes Fenster, und klicke
Es ist der Erwartungswert
Lösungs-Hinweise 1. Übung
- Beschreibende Statistik & Verteilungsfunktion -
1. Die folgende Tabelle enthält die Pulsfrequenz einer
Versuchsgruppe von 39 Personen:
| 88 | 76 | 84 | 64 | 60 | 64 | 60 | 64 | 68 | 74 | 68 | 68 | 72 |
| 76 | 72 | 52 | 72 | 64 | 60 | 56 | 72 | 88 | 80 | 76 | 64 | 72 |
| 60 | 76 | 88 | 72 | 64 | 60 | 60 | 72 | 92 | 80 | 72 | 64 | 68 |
a) Geben Sie eine Tabelle mit den absoluten und relativen
Häufigkeiten an und bestimmen Sie statistische Maßzahlen wie
Mittelwert, Median, Modalwert, Spannweite, sowie Streuungsmaße wie Varianz,
St.Abweichung, Schiefe, Wölbung.
- Eintippen der Daten in einer Spalte des SPSS Datenfensters
![]() auf Var0001 öffnet
Fenster,
welches Änderung des Variablennamens z.B. in puls gestattet.
auf Var0001 öffnet
Fenster,
welches Änderung des Variablennamens z.B. in puls gestattet.
![]() öffnet Fenster,
öffnet Fenster,
welches die deskriptive Statistik ermöglicht.
Schiebe puls in rechtes Fenster, und klicke ![]() an:
Mittelwert, Median, Modalwert, Spannweite, sowie Streuungsmaße wie
Varianz,
St.Abweichung, Schiefe, Wölbung sind nun nur noch anzuklicken und das
Befehlsfenster auszuführen.
an:
Mittelwert, Median, Modalwert, Spannweite, sowie Streuungsmaße wie
Varianz,
St.Abweichung, Schiefe, Wölbung sind nun nur noch anzuklicken und das
Befehlsfenster auszuführen.
Es ist der Erwartungswert
b) Zeichnen Sie Linien-, Balken-, Kreis- und
Fächendiagramme.
Unter ![]() stehen die entsprechenden
Befehle bereit.
Beachten Sie, daß entweder Kategorien oder Einzelwerte über
der x-Achse dargestellt werden sollten!
stehen die entsprechenden
Befehle bereit.
Beachten Sie, daß entweder Kategorien oder Einzelwerte über
der x-Achse dargestellt werden sollten!
![]() .
.
Zeichnen Sie das Histogramm:
Unter ![]() stehen der
entsprechende Befehle bereit.
Selbstständig wird von SPSS eine Klasseneinteilung vorgenommen.
stehen der
entsprechende Befehle bereit.
Selbstständig wird von SPSS eine Klasseneinteilung vorgenommen.
Soll diese geändert werden, so ![]() ,
und es erscheint neues Fenster:
,
und es erscheint neues Fenster:
![]()
![]()
Es erscheint neues Fenster, in dem der Benutzer mit dem Punkt
![]() weitergeführt wird:
Die gewünschte Achseneinteilung kann eingestellt werden.
weitergeführt wird:
Die gewünschte Achseneinteilung kann eingestellt werden.
Bei einem etwas "nicht-normalverteiltem" Histogramm sollte man
mehrere Varianten der Klasseneinteilung probieren!
c) Gruppieren Sie die Daten in 5 Klassen und zeichnen Sie
erneut Histogramm, Linien-, Balken-, Kreis- und Fächendiagramme.
Zuerst muß eine Klassifizierungsvariable erstellt werden; dazu gibt es
zwei Möglichkeiten:
![]()
ermöglicht unter Benutzung der
![]() eine selektive
Besetzung einer Klassifizierungsvariablen.
eine selektive
Besetzung einer Klassifizierungsvariablen.
![]()
ermöglicht die selektive Besetzung einer
Klassifizierungsvariablen in einem Fenster: Variable puls ist ins mittlere
Fenster zu schieben, und ein Name für die Ausgangsvariable zu wählen.
Der Button ![]() ermöglicht die selektive
Zuweisung von Werten zur Klassifizierungsvariablen. Nach einer Zuweisung darf
nicht der Ausführungs-Befehl
ermöglicht die selektive
Zuweisung von Werten zur Klassifizierungsvariablen. Nach einer Zuweisung darf
nicht der Ausführungs-Befehl ![]() vergessen werden!
vergessen werden!
( Bemerkung: -![]() Klick auf Transformieren -
Klick auf Transformieren -![]() Klick auf
Variable kategorisieren
Klick auf
Variable kategorisieren
ermöglicht die automatische Besetzung einer Variablen, die Percentile
ergibt, also Klassen etwa gleich vieler Werte. Dies ist hier nicht gemeint.
)
Unter ![]() kann ein neues Datenfile erzeugt werden, das dann die gruppierten Daten
beschreibt.
Man schiebt dazu die Klassifizierungsvariable in die Zeile der
Break-Variablen,
sowie Variable puls ins Klassifizierungsfenster,
und klickt an daß die Fallzahl je Break-Gruppe gespeichert
werden soll, und daß eine neue Datei erzeugt werden soll. Voreingestellt
heißt diese Datei AGGR.sav, der Name kann in einem Fenster
geändert werden. (Eine Labelvariable kann extra zur Beschreibung der
Klassifizierungsvariablen verwendet werden. Diese erscheint dann z.B. in
Grafiken.)
kann ein neues Datenfile erzeugt werden, das dann die gruppierten Daten
beschreibt.
Man schiebt dazu die Klassifizierungsvariable in die Zeile der
Break-Variablen,
sowie Variable puls ins Klassifizierungsfenster,
und klickt an daß die Fallzahl je Break-Gruppe gespeichert
werden soll, und daß eine neue Datei erzeugt werden soll. Voreingestellt
heißt diese Datei AGGR.sav, der Name kann in einem Fenster
geändert werden. (Eine Labelvariable kann extra zur Beschreibung der
Klassifizierungsvariablen verwendet werden. Diese erscheint dann z.B. in
Grafiken.)
d) Bestimmen Sie für die Ausgangsdaten die
empirische Verteilung und zeichnen Sie diese in einem Koordinatensystem.
Die Tabelle mit den relativen Häufigkeiten ![]() ist zu verstehen als
die diskrete Dichte der Wahrscheinlichkeiten des Auftretens entsprechender
Ausprägungen der Puls-Variable X (der Kategorie).
ist zu verstehen als
die diskrete Dichte der Wahrscheinlichkeiten des Auftretens entsprechender
Ausprägungen der Puls-Variable X (der Kategorie).
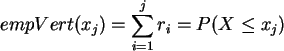
2. Die Zufallsvariable X sei die Augenzahl eines ausgespielten
Würfels mit den möglichen Realisationen der
Augen zu { 0, 1, 2, 3, 4, 5 }. Der Würfel sei "ehrlich", d.h. es
gelte
![]() .
.
Die Zufallsvariable Y sei das Resultat von fünf Münzwürfen,
wobei jeweils die "Zahl" gezählt werde.
Offenbar hat Y die gleichen Realisationen.
Man gehe davon aus, daß Y
binomialverteilt ist mit p=1/2, also
- Eintippen der Daten: Realisierung, P(X=k), und P(Y=k) in
je einer Spalte des SPSS Datenfensters
![]() auf Var0001, Var0002 oder Var0003 öffnet
je ein
Fenster, welches Änderung des Variablennamens z.B. in real, px, py
gestattet. Dabei kann beim Eintippen px=1, und py={1,5,10,10,5,1}
gesetzt werden, und in
auf Var0001, Var0002 oder Var0003 öffnet
je ein
Fenster, welches Änderung des Variablennamens z.B. in real, px, py
gestattet. Dabei kann beim Eintippen px=1, und py={1,5,10,10,5,1}
gesetzt werden, und in
![]() kann dann px/6 bzw. py/32 berechnet werden.
kann dann px/6 bzw. py/32 berechnet werden.
Unter ![]() und
und ![]() können beide Dichten gleichzeitig gezeigt werden.
können beide Dichten gleichzeitig gezeigt werden.
Berechnen Sie Mittelwert und Streuung für X
und für Y. (Stimmt die 3![]() -Regel?)
-Regel?)
Es ist
der Erwartungswert von X
Nimmt man für X je
6 Versuche an, und für Y je 32 Versuche, so kann man mittels SPSS
mit Gewichten arbeiten. Vergleichen Sie so berechnete Mittelwerte
und Streuungen.
Mit
![]() öffnet sich Fenster, welches die deskriptive Statistik ermöglicht.
Schiebe Variable real in rechtes Fenster, und klicke
öffnet sich Fenster, welches die deskriptive Statistik ermöglicht.
Schiebe Variable real in rechtes Fenster, und klicke ![]() an:
jetzt nur Mittelwert und Varianz anklicken.
an:
jetzt nur Mittelwert und Varianz anklicken.
Das Resultat ist Ex = Mittelwert![]() =2,5 ,
aber unter Varianz erscheint der Wert 3,5. !??!
=2,5 ,
aber unter Varianz erscheint der Wert 3,5. !??!
Da wir hier direkt mit 6 Werten der Realisierung arbeiten, ist n=6 die Zahl der
bearbeiteten Fälle, und SPSS gibt ![]() aus, d.h. um
aus, d.h. um
![]() zu erhalten, müssen wir mit 5/6 multiplizieren: das
ergibt das schon bekannte Resultat von 2,92 .
zu erhalten, müssen wir mit 5/6 multiplizieren: das
ergibt das schon bekannte Resultat von 2,92 .
Für Y erzeugen wir eine neue Spalte mit "Gewichten", die größer als
Eins sein sollen.
Also kann die Spalte py mit 32 multipliziert werden.
Unter ![]() und
und ![]()
kann nun diese Variable
als Gewicht für weitere Berechnungen verwendet werden. Dabei wird so
verfahren, als ob jeder Wert der Realisierung so oft auftritt, wie sein Gewicht
angibt. (Man könnte also auch 32 Zeilen erzeugen, mit den entsprechenden
Werten von real: einmal 0, fünfmal 1, usw.)
Mit den analogen Befehlen
![]() schiebe wieder Variable real in rechtes Fenster, und klicke
schiebe wieder Variable real in rechtes Fenster, und klicke ![]() an:
Mittelwert und Varianz anklicken.
Dies gibt dann
das Resultat Ey = Mittelwert
an:
Mittelwert und Varianz anklicken.
Dies gibt dann
das Resultat Ey = Mittelwert![]() =2,5 , also gleich dem von X,
aber unter Varianz erscheint nun der Wert 1,29 !
=2,5 , also gleich dem von X,
aber unter Varianz erscheint nun der Wert 1,29 !
Da wir nun mit 32 Werten als Summe der Gewichte der Realisierung arbeiten,
ist n=32 die Zahl der
bearbeiteten Fälle, und SPSS gibt ![]() aus, d.h. um
aus, d.h. um
![]() zu erhalten, müssen wir mit 31/32 multiplizieren:
dies gibt das schon
bekannte Resultat von 1.25 .
zu erhalten, müssen wir mit 31/32 multiplizieren:
dies gibt das schon
bekannte Resultat von 1.25 .
Also
![]()
(Anhang:
Die Verteilungsfunktion der Binomialverteilung ist in SPSS verfügbar:
![]() und im Fenster
Funktionen auswählen
und im Fenster
Funktionen auswählen ![]() .
Dabei ist hier q der Wert der Realisierung, n der Exponent der
Binomialformel, also n=5, und p die Wahrscheinlichkeit des einzelnen
Bernoulliversuches, also hier p=0.5. Im der Berechnungszeile muß dann
letztlich stehen: CDF.BINOM(real,5,0.5) .
(CDF bedeutet cumulative density function) )
.
Dabei ist hier q der Wert der Realisierung, n der Exponent der
Binomialformel, also n=5, und p die Wahrscheinlichkeit des einzelnen
Bernoulliversuches, also hier p=0.5. Im der Berechnungszeile muß dann
letztlich stehen: CDF.BINOM(real,5,0.5) .
(CDF bedeutet cumulative density function) )