Aufgabe 1
Das Kohlenstoff-Isotop 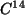 hat eine Halbwertzeit von 5730 Jahren.
Sein Anteil in lebenden Organismen entspricht seinem Anteil am Kohlenstoff
in der Luft, der sich über Jahrtausende nicht verändert hat. Stirbt ein
Organismus ab, so zerfällt das in ihm gebundene Kohlenstoff-Isotop
hat eine Halbwertzeit von 5730 Jahren.
Sein Anteil in lebenden Organismen entspricht seinem Anteil am Kohlenstoff
in der Luft, der sich über Jahrtausende nicht verändert hat. Stirbt ein
Organismus ab, so zerfällt das in ihm gebundene Kohlenstoff-Isotop
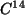 . Wie alt ist nun ein Papyrus, der noch
. Wie alt ist nun ein Papyrus, der noch 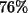 des
des 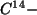 Isotops
enthält, den ein heutig gefertigter Papyrus hätte?
Isotops
enthält, den ein heutig gefertigter Papyrus hätte?
Hinweis: Der Zerfall wird durch die Funktion
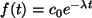 mit
mit 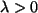 modelliert.
modelliert.
Lösung zu Aufgabe 1 (5 Punkte)
Bestimmung der Konstanten
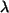
:
Es gilt
Nach Division dieser Gleichung durch
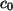
und Logarithmieren folgt
Bestimmung des Alters
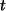
:
Es gilt
Also folgt
Somit ist das Alter 2269 Jahre.
Lösung zu Aufgabe 2 (11 Punkte)
a) Nach einer Minute verringert sich die Anzahl in A um
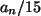
und
vermehrt sich um
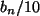
. Also gilt
d. h. (
1) ist erfüllt.
b) Wegen
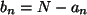
erhalten wir aus (
1)
also (
2).
Dies ist ein inhomogenes lineares Modell mit
c) Da
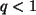
existiert der Grenzwert
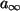
und berechnet sich nach
d) Es gilt nach n Minuten
Es soll die Ungleichung
gelten. Dies ist gleichwertig mit
Nach Umformung erhalten wir
Nach Logarithmieren ergibt sich
Es sind also 9 Minuten nötig .
Lösung zu Aufgabe 3 (15 Punkte)
a) Es gilt
Offenbar gilt
genau dann, wenn
b)
Die Folge ist für
nicht negativ.
c) Auf Grund der Abbildung 1 ist die Folge für alle Anfangswerte aus dem
Intervall
konvergent.
Wegen
ist der Fixpunnkt
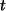
anziehend.
(i) Für
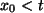
wächst die Folge monoton bis
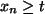
. Ist
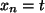
, so
bleibt die Folge konstant. Ist
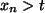
, so springt die
Folge zu
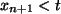
und es wiederholt sich das Verhalten zu Beginn.
(ii) Ist
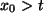
, so springt die
Folge zu
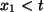
und es wiederholt sich das Verhalten zu Beginn des
Falles (i).
(iii) Für
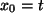
gilt
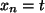
für alle n.
e) Die Ungleichung
ist gleichwertig mit
oder nach Umformen
Lösung zu Aufgabe 4 (20 Punkte)
a)
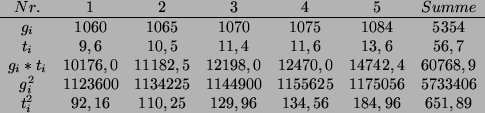
Wir erstellen folgende Tabelle
Wir bestimmen nun die beste Anpassung
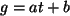
. Es gilt
Weiter gilt
Die beste Anpassung lautet also
Wir bestimmen zunächst
Für den Korrelationskoeffizient ergibt sich
b) Wir bestimmen die beste Anpassung
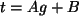
. Es gilt dann
Weiter gilt
Die beste Anpassung lautet also
Dies ist gleichwertig mit der Gleichung
Der Korrelationskoeffizient verändert sich nicht, da
Die Gerade ist in Abbildung 2 dargestellt.
c) Die Geraden schneiden sich im Schwerpunkt
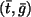
, also
d) Der fragliche Punkt wandert zur besten Anpassung (i).
Folglich wird die lineare Anpassung besser.
Aufgabe 5
Beim Auszählen von Zellen in 50 Quadranten eines Hämozytometers ergab sich
folgende Häufigkeitstabelle.
a)
Bestimmen Sie folgende Charakteristiken: den Modalwert,
den Mittelwert, die empirische Varianz 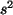 und das Quantil der Ordnung
und das Quantil der Ordnung
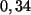 .
.
b) Bestimmen Sie die Ausreißer und dann die Kenngrößen des Boxplots.
Zeichnen Sie den Boxplot.
c) Zeichnen Sie die empirische Verteilungsfunktion.
Lösung zu Aufgabe 5 (15 Punkte)
a)
Der Modalwert ist als Wert mit der größten Häufigkeit gleich 4.
Es gilt mit
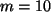
und
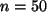
Es gilt
Also folgt
Wir berechnen zunächst die empirische Verteilungsfunktion
Weiter gilt
Also folgt
Somit
b)
Aus der letzten Tabelle lesen wir die Quartile ab.
Wir definieren die Größen
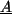
und
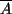
Folglich ist 11 ein Ausreißer. Wir eleminieren diesen Wert und erhalten die
Häufigkeitstabelle mit der empirischen Verteilungsfuntion
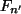
Hieraus ergeben sich die Quartile aus der Tabelle:
Der Boxplot ist in Abbildung 3 enthalten.
c) Die empirische Verteilungsfunktion ist in Abbildung 4 dargestellt.
Aufgabe 6
a) Wie viel Möglichkeiten gibt es,
9 verschiedenfarbige Perlen auf einer Kette anzuordnen?
b) Wie viele Möglichkeiten gibt es,
3 rote, 4 weiße und 2 grüne Perlen auf einer Schnur
aufzureihen?
Lösung zu Aufgabe 6 (4 Punkte)
a) Es gibt
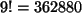
Möglichkeiten.
b) Es gibt
Möglichkeiten.
Manfred Riedel
2002-08-14
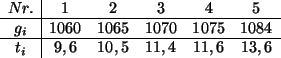
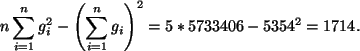
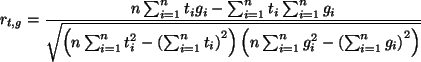
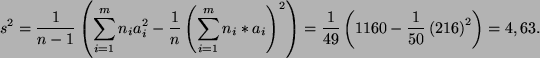
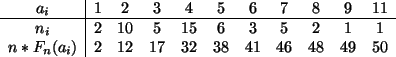
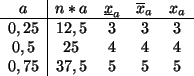
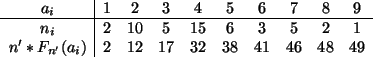
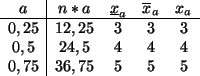
![\includegraphics[width=16cm,angle=0]{null.ps}](img105.png)
![\includegraphics[width=16cm,angle=0]{ein.ps}](img106.png)