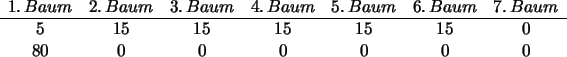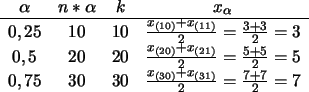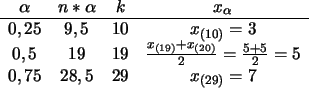Aufgabe 1
Jährlich werde (periodisch) die Masse
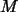 des Cäsiumisotops
des Cäsiumisotops 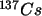 an die Umgebung abgegeben.
(Beginnend mit
an die Umgebung abgegeben.
(Beginnend mit 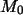 =
=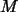 .) Das Cäsium verliert (ebenfalls jährlich)
.) Das Cäsium verliert (ebenfalls jährlich)
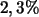 seiner Masse durch radioaktiven Zerfall.
Es bezeichne
seiner Masse durch radioaktiven Zerfall.
Es bezeichne 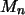 die Gesamtmasse von
die Gesamtmasse von 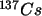 am Ende des n-ten Jahres.
am Ende des n-ten Jahres.
a) Zeigen Sie, dass die Folge
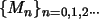 einem
inhomogenen linearen Modell der Populationsentwicklung genügt und geben Sie
die entsprechenden Parameter
einem
inhomogenen linearen Modell der Populationsentwicklung genügt und geben Sie
die entsprechenden Parameter 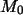 ,
, 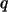 und
und 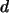 an.
an.
b) Bestimmen Sie die Grenzkonzentration 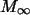 und
und 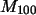 .
.
Lösung 1
a) Am Ende des ersten Jahres sind noch
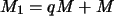
vorhanden, wobei
gilt,
und am Ende des zweiten Jahres haben wir
Analog folgt
Es liegt also ein Populationsmodell mit
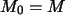
,
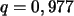
und
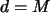
vor.
b) Es gilt dann
Außerdem folgt
Aufgabe 2
Phosphor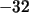 hat eine Halbwertszeit von 14,2 Tagen. Wie lange dauert
es (Angabe in Stunden, Minuten und Sekunden), dass eine Probe
hat eine Halbwertszeit von 14,2 Tagen. Wie lange dauert
es (Angabe in Stunden, Minuten und Sekunden), dass eine Probe 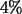 ihrer Masse verliert?
ihrer Masse verliert?
Hinweis: Der Zerfall wird durch die Funktion
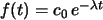 mit
mit 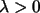 modelliert.
modelliert.
Lösung 2
Es gilt
Dividiert man durch
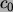
und bildet den natürlichen Logarithmus auf beiden
Seiten der Gleichung, so folgt
also ist
Nach Aufgabenstellung erhält man den Ansatz
Geht man analog vor, so folgt die gesuchte Zeit (in Tagen):
Das sind 20 Stunden 4 Minuten und 15 Sekunden.
Aufgabe 3
Zur Rast lassen sich 80 Stare auf 7 Bäumen nieder. Die Stare lassen sich nicht unterscheiden.
a) Geben Sie 2 mögliche Verteilungen der Stare auf den Bäumen an.
b) Berechnen Sie die Anzahl der Verteilungen der Stare auf den Bäumen und geben Sie an mit welcher kombinatorischen Größe die Anzahl berechnet wird.
Lösung 3
a) Folgende Tabelle enthält zwei Lösungen
b) Die Bäume kann man als Zellen und die Stare als nichtunterscheidbare Kugeln
interpretieren. So ist jede Aufteilung eine Aufteilung von
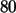
Kugeln auf
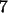
Zellen. Dies sind alle Kombinationen von
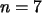
zu
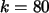
(mit Wiederholung), also
Möglichkeiten.
Aufgabe 4
Es sei die Folge
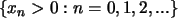 rekursiv gegeben durch
rekursiv gegeben durch
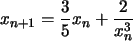 und
und
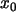 .
.
a) Bestimmen Sie die
Reproduktionsfunktion 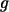 dieser Folge und ihren Fixpunkt
dieser Folge und ihren Fixpunkt 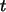 .
.
b) Zeichnen Sie in einem Koordinatensystem die Reproduktionsfunktion,
ihren Fixpunkt und drei Werte der Folge mit Anfangswert
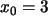 . Zeichnen Sie den Kurvenzug ein, der die drei Werte darstellt.
. Zeichnen Sie den Kurvenzug ein, der die drei Werte darstellt.
c) Zeigen Sie, dass der Fixpunkt anziehend ist.
d) Bestimmen Sie alle Anfangswerte 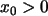 ,
für die die Folge konstant ist.
,
für die die Folge konstant ist.
Lösung 4
a) Die Reproduktionsfunktion lautet
Der Fixpunkt
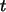
erfüllt die Gleichung
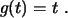 |
|
|
(1) |
Wird von dieser Gleichung (von beiden Seiten)
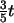
subtrahiert,
und durch
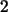
dividiert, so ergibt sich
Daraus folgt
b)
Die Populationsentwicklung ist in Bild 1 dargestellt.
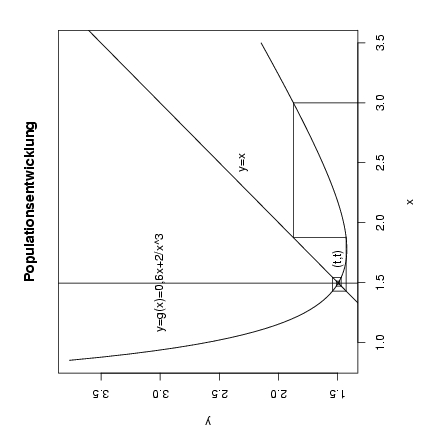
c) Es gilt
Somit gilt
also ist der Fixpunkt
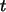
anziehend.
d) Wenn alle Glieder der Folge konstant bleiben, muss der Anfangswert ein Fixpunkt sein, d. h. es gilt
Lösung 5
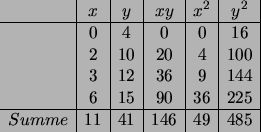
Folgende Tabelle enthält Hilfsresultate zur Berechnung der
Korrelationskoeffizienten:
Es ergibt sich nun der Korrelationskoeffizient aus
Für die beste Anpassung
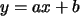
von
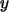
durch

werden die Parameter aus
und aus
ermittelt.
Die beste Anpassung hat die Gestalt
b)
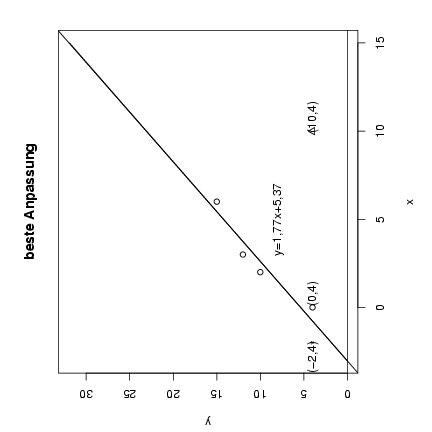
Wenn
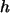
verändert wird, so wandert der Punkt
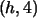
auf
der Geraden
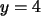
. Auf Grund der Zeichnung
ist zu vermuten, dass im Falle
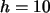
die lineare Anpassung schlechter ist als bei
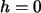
.
c) Die Summe der quadratischen Residuen für
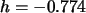
ist kleiner als in Teilaufgabe a), da dann
ist und folglich
ein Summand null wird. Für dieses
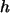
wird also das Bestimmheitsmaß größer als in a).
Lösung 6
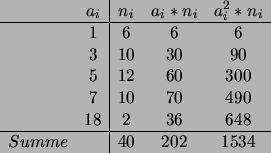
Zur Bestimmung von
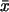
und
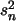
dient folgende Tabelle:
Also ergeben sich mit n=40
Zur Bestimmung des Quantils der Ordnung
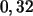
bildet man
Die nächste größere ganze Zahl ist
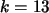
. Es gilt dann
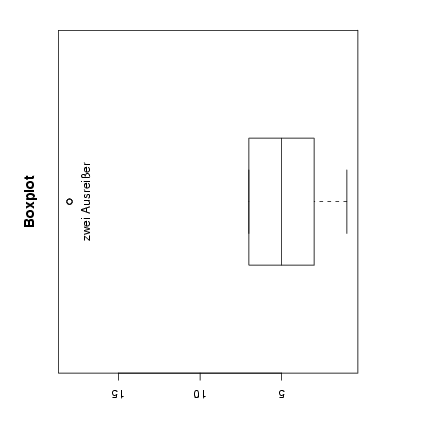
b) Durch folgende Tabelle bestimmt man die Quantile:
Es gilt für die Grenzen:
Somit sind die beiden Werte 18 Ausreißer.
Durch folgende Tabelle bestimmt man die Quantile nach Elimination der
Ausreißer mit n=38:
Also ändern sich die Quantile hier nicht.
Dr.Wolfgang Quapp
2003-07-14