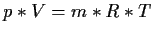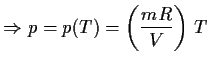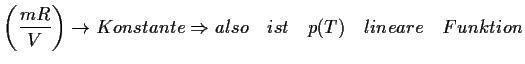(a) ![]() , (b)
, (b) ![]() , (c)
, (c) ![]() , (d)
, (d)
![]() , (e)
, (e)
![]() , (f)
, (f)
![]() , (g)
, (g)
![]() , (h)
, (h)
![]() ,
(i)
,
(i)
![]() , (j)
, (j)
![]() , (k)
, (k)
![]() , (l)
, (l) ![]() , (m)
, (m)
![]() , (n)
, (n)
![]() , (o)
, (o)
![]() , (p)
, (p)
![]() , (q)
, (q)
![]() , (r)
, (r)
![]() .
.
Lösung:
- a)
-
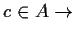 wahr
wahr - b)
-
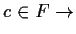 falsch
falsch - c)
-
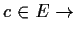 falsch
falsch - d)
-
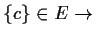 wahr
wahr - e)
-
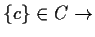 falsch, aber es ist
falsch, aber es ist
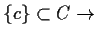 wahr
wahr - f)
-
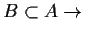 wahr
wahr - g)
-
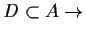 wahr
wahr - h)
-
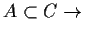 falsch
falsch - i)
-
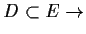 falsch, weil
falsch, weil 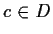 kein Element von
kein Element von 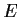 ist.
ist. - j)
-
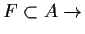 wahr
wahr - k)
-
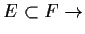 falsch
falsch - l)
-
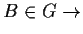 wahr
wahr - m)
-
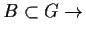 falsch
falsch - n)
-
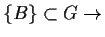 wahr
wahr - o)
-
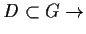 falsch
falsch - p)
-
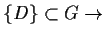 wahr
wahr - q)
-
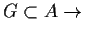 falsch
falsch - r)
-
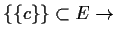 wahr
wahr
- a)
-
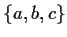 ,
, - b)
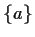 ,
,- c)
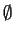 ,
,- d)
-
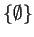 .
.
- a)
-
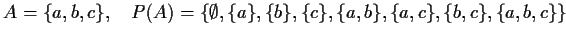
damit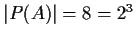
- b)
-
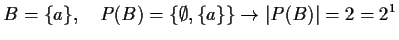
- c)
-
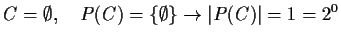
- d)
-
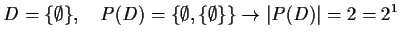
Was sind (i) ![]() , (ii)
, (ii) ![]() , (iii)
, (iii)
![]() ,
(iv)
,
(iv) ![]() , (v)
, (v)
![]() , (vi)
, (vi)
![]() ,
(vii)
,
(vii)
![]() ?
?
Lösung:
- (i)
-
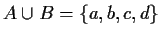
- (ii)
-
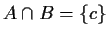
- (iii)
-
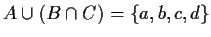
- (iv)
-
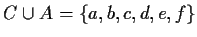
- (v)
-
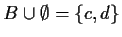
- (vi)
-
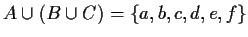
- (vii)
-
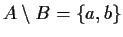
- a)
- Gegeben sei die Abbildung
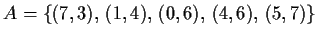 . Geben Sie den Definitions- und Wertebereich an. Ist die Abbildung
. Geben Sie den Definitions- und Wertebereich an. Ist die Abbildung
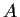 eineindeutig, eindeutig oder keines von beiden?
eineindeutig, eindeutig oder keines von beiden?
Lösung:A meint
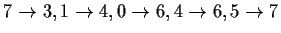
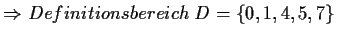 A ist eindeutig, da jedem Urbild ein Bild zugeordnet wird
A ist eindeutig, da jedem Urbild ein Bild zugeordnet wird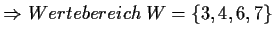
A ist nicht eineindeutig, da dem Bild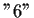 zwei Urbilder
zugeordnet werden
zwei Urbilder
zugeordnet werden
- b)
- Modellieren Sie die folgenden Sachverhalte durch eine
Abbildung. Beschreiben Sie Definitionsbereich, Wertebereich, Bilder und
Urbilder näher.
- (i)
- Von einer chemischen Substanz stehen 12 (gleiche)
Mengeneinheiten zum Verkauf
bereit. Beim Verkauf einer Mengeneinheit der Substanz wird ein Erlös von
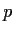 Geldeinheiten erzielt. Der (Gesamt)-Erlös wird in Abhängigkeit von der Anzahl g
der verkauften Mengeneinheiten
Geldeinheiten erzielt. Der (Gesamt)-Erlös wird in Abhängigkeit von der Anzahl g
der verkauften Mengeneinheiten
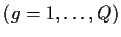 ermittelt.
ermittelt.
Lösung:
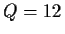 Mengeneinheiten,
Verkauf: Preis p, Menge q
Mengeneinheiten,
Verkauf: Preis p, Menge q
Erlös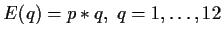 ,
,
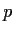 =Anstieg der linearen Funktion
=Anstieg der linearen Funktion 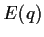
- (ii)
- In einem geschlossenen Behälter mit konstantem Volumen befindet
sich ein Gas, das Temperaturschwankungen im Bereich von
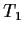 bis
bis 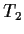 unterworfen wird. Der Druck des Gases wird in Abhängigkeit von der
Temperatur gemessen.
unterworfen wird. Der Druck des Gases wird in Abhängigkeit von der
Temperatur gemessen.
Lösung:Druck: Zustandsgleichung für ideales Gas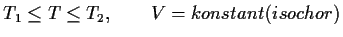
m: Gasmasse, R: spezielle Gaskonstante