Formeln zur linearen Regression:
Definiert man die Summe der Fehlerquadrate einer besten Funktion
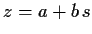 zu
zu
so ergeben sich als partielle Ableitungen nach den Parametern der Gerade die
linearen Gleichungen:
und
Die Lösung ist
und
Aus den Formeln ergibt sich noch der Korrelationskoeffizient:
und die minimale Fehlerquadratsumme:
Mit den Mittelwerten
und
wird daraus kürzer:
und
sowie
Der Punkt
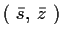 ist der Schnittpunkt der
Regressionsgraden
ist der Schnittpunkt der
Regressionsgraden 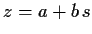 mit der invertierten Graden
mit der invertierten Graden
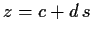 , die aus
, die aus 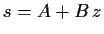 entsteht:
entsteht:
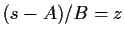 , also
, also 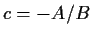 und
und 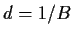 .
.
Im Beispiel ist
a= -19.05, b= 5.07, A= 4.10, B = 0.19, also 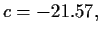 und
und 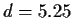
mit
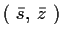 = ( 14.2, 53.0 ) .
Der Winkel zwischen den Graden ist
= ( 14.2, 53.0 ) .
Der Winkel zwischen den Graden ist
mit den
Anstiegen der beiden Graden als 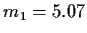 , und
, und 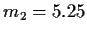 ergibt sich
ergibt sich
Dr.Wolfgang Quapp
2003-05-27
![]() zu
zu
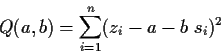
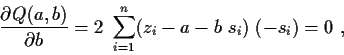
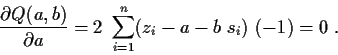
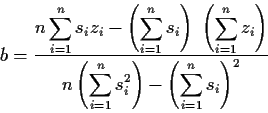
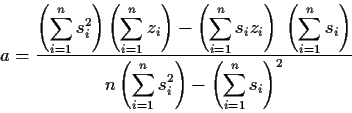
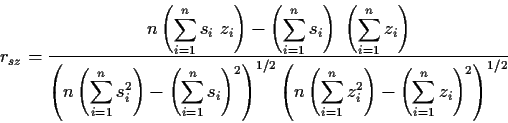
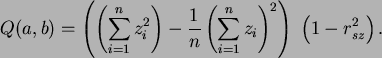
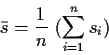
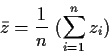
![]() und
und ![]()
![]() = ( 14.2, 53.0 ) .
Der Winkel zwischen den Graden ist
= ( 14.2, 53.0 ) .
Der Winkel zwischen den Graden ist